Publicaciones Recientes
Segmentos Dirigidos
Este concepto se oye mucho en las Olimpiadas de Matemáticas, pero --como muchos otros de olimpiada-- no es un tema que se enseñe en bachillerato. Esto puede llegar a asustar a muchos estudiantes, pero en realidad es un tema al que nada hay que temerle. Es muy fácil de entender y sobre todo es muy útil.
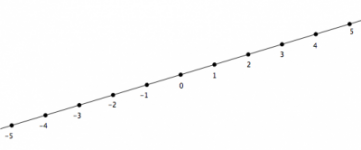
La idea principal de los segmento dirigidos es agregar una propiedad extra a la noción de segmento. Esta propiedad se resume así:
ciudades y sedes: actualización
Por favor vean las sedes del concurso ciudades en este link (archivo xls): OMM 2008 Tam: Ciudades, sedes, planteles.
En los links del final está la convocatoria actualizada OMM 2008 en Tamaulipas: los cambios son la fecha del concurso ciudades y la cancelación del concurso en Valle Hermoso, así como cambios de sede.
Concurso Ciudades: en stand by, excepto San Fernando
Sólo para actualizar la información sobre la etapa ciudades de la OMM tamaulipeca:
1)El primer concurso de ciudades se realizará el día 25 de abril en el CBTis 129 de San Fernando. Por favor quienes estén interesados en participar de Matamoros, Valle Hermoso o Reynosa (o de Jiménez) por favor soliciten información más precisa a ese plantel.
Convocatoria OMM en Tamaulipas
Debido a ciertos contratiempos --económicos, y de otro tipo--la liberación de la convocatoria se retrasó mucho más de lo que esperábamos. Esta delegación libera hoy la convocatoria esperando que el concurso ciudades se pueda organizar en el tiempo disponible (tres semanas).
Los planteles sede apenas se están proponiendo y en el transcurso de la semana se confirmará su aceptación.
Concurso ONMAS Tamaulipas (resultados)
La VIII Olimpiada Nacional de Matemáticas para alumnos de Secundaria (ONMAS) --en su etapa estatal Tamaulipas-- se llevó a cabo en las instalaciones de la UAMCEH-UAT el día 28 de marzo de 2008.
Los organizadores (Luis Carrera de UPN Victoria, Ramón J Llanos P y José Muñoz D de la UAMCEH-UAT) se congratulan de ver el interés de los adolescentes tamaulipecos por las matemáticas.
Siete enteros
En cualquier conjunto de siete enteros siempre hay dos cuya suma o diferencia es múltiplo de 11.
Aguántenme el corte y ONMAS
Les informo que el proceso de selección de la OMM en Tamaulipas no ha podido despegar como debiera por razone$ de pe$o.
Pero es muy posible que el 20 de abril sea el concurso de ciudades. Después de vacaciones les informo de las sedes. (Y si no hubiera ciudades, nos pasamos a regiones en mayo :(
Por lo pronto y para ocupar nuestro tiempo libre estamos organizando el concurso de la olimpiada de secundarias (ONMAS) para llevar una selección Tamaulipas a Colima en mayo.
Estos eran dos amigos...
B: Ah…Mmhh… Creo que esa sí me la sé. Es base por altura. ¿Cierto?
A: ¿Pero si no te dan la altura?
B: Bueno, pues ¿qué te dan?
A: Te dan las longitudes de los lados.
B: Bueno, entonces saco la altura con el seno del ángulo ¿te dan un ángulo?
A: No.
B: Ah pues deja ver…Creo que se puede eliminar el seno utilizando la ley de cosenos… eso lo hice una vez cuando estudié la secundaria… Deja ver si me sale…
$2(ABC) = ah = absenC$ ¿OK?
A: Con $(ABC)$ estás denotando el área del triángulo $ABC$ ¿no es así?

Problema, semana 18-22 de Feb.
Longitud Mínima
Sea ABC un triángulo y P un punto que se mueve sobre la recta que contiene al lado BC. Consideremos M y N los pies de las perpendiculares trazadas desde P sobre los lado AB y AC respectivamente. Encuentra el punto P para el cual MN tiene longitud mínima.
