Publicaciones Recientes
Problema de coolinealidad
Sean C1,C2,C3 tres circunferencias tangentes exteriores dos a dos. Definamos los siguientes puntos; R=C1∩C2 S=C1∩C3 y T=C2∩C3 , sean X,Y los puntos sobre C2,C3 de modo que XY sea la tangente comun y esta no pase por C1. Sea J la interseccion de la tangente a C1,C2 por R y a la tangente comun a C1,C3 por S.
Áreas iguales en un trapecio
Demuestra que para cualquier trapecio ABCD, las áreas de las triángulos sombreados son iguales.
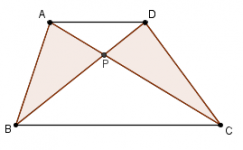
Sumas
Considere las sumas
S=4⋅5−5⋅6+…−2009⋅2010
T=3⋅6−4⋅7+…−2008⋅2011
Calcular el valor de S−T
Mayo 29, Etapa Regional de la XXIII OMM Tamaulipas
La región sur decidió unirse a la centro y norte y aplicará el examen de la etapa regional el día 29 de mayo. Así que en las tres regiones el concurso regiones será el día 29 de mayo.

Producto de diagonales en un polígono regular
Sea A1,A2,…,An los n vértices de un polígono regular con circunferencia circuncrita de radio R, Demuestra que:
OMM Tamaulipas: concurso regional aplazado
Posiblemente hasta el 29 de mayo, el concurso regional entra en una fase de espera debido a la alerta sanitaria nacional --con lo cual, el estatal se aplazaría hasta el 26 de junio.
Encontrar las soluciones de la igualdad
Encuentre todos los números primos p,q tales que p+q = (p−q)3.
Fecha del concurso regiones, decisión de cada sede...
--pero conviene mantener la hipótesis de que se realizará el viernes 8 según programa. (Excepto para la región sur que lo realizará el 22 de mayo... y quizá las otras dos secundemos la propuesta del CETis 109)
Isósceles semejantes sobre un triángulo
Consideremos A′, B′ y C′ tres puntos en el exterior del triángulo ABC, de tal manera que los triángulos A′BC, AB′C y ABC′ son todos isósceles semejantes y de bases BC, CA y AB respectivamente, Demuestra que AA′, BB′ y CC′ concurren.
Equiláteros en los lados de un triángulo
Este es un problema con la misma figura del triángulo de napoleón.
Consideremos los puntos A′, B′ y C′ puntos fuera del triángulos ABC de tal manera que los triángulos A′BC, AB′C y ABC′ son equiláteros. Demuestra que AA′, BB′ y CC′ concurren y son de la misma longitud.
