Publicaciones Recientes
ayuda porfavor urgente geometria analitica
¿Quien me ayda con este problema? porfiss
.-Dos de los vertices de un tringulo equilatero son los puntos a(-3,1), b(1,1) hayar las cordenadas del 3er vertice ...
Un problema de geometría --de Wong Yan Loi
En su libro Introduction to geometry, Wong Yan Loi presenta el problema motivo de este post (y lo resuelve con geometría analítica). La redacción del enunciado está aquí ligeramente modificada y a la solución le he añadido explicaciones que Wong Yan Loi se ahorra. (Me gustaría ver una solución sintética de este problema. Si alguien la encuentra sería una buena obra que la compartiera con los lectores de MaTeTaM.)
El 5 del VI concurso nacional OMM 1992
Cuando llueve, como en estos días que se formó en el Golfo de México la tormenta Ingrid, me pongo inspirado y con ganas de postear. Buscando qué hacer mientras llovía me encontré con este problema del concurso nacional de 1992 (VI OMM).
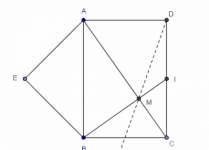
Teorema fundamental de la proporcionalidad (Tales)
Si una recta paralela al lado $BC$ del triángulo $ABC$ corta en $B'$ a $AB$ y en $C'$ a $AC$), entonces $$\frac{AB}{AB'}=\frac{AC}{AC'}=\frac{BC}{B'C'}$$
Este es el Teorema de Tales para triángulos del cual hemos hablado ya en MaTeTaM. En esta oportunidad comentaré el teorema particularizado para triángulos rectángulos y lo demostraré con el método de áreas.
Convocatoria OMM Tamaulipas 2013
La etapa regional de la Olimpiada Mexicana de Matemáticas (OMM) Tamaulipas 2013, se celebrará en 9 ciudades sede el día 27 de septiembre. Atacho convocatoria oficial (firmas en proceso).
Nuevo Laredo CONALEP No 246
Reynosa Reynosa ITACE
Matamoros CONALEP 55
San Fernando CBTis No 129
Ciudad Victoria COBAT Plantel 05
Soto La Marina COBAT Plantel 16
Jaumave CBTis No 210
Mante CBTis No 15
Madero CETis No 109
El examen de la etapa estatal se aplicará en el CBtis 15 de Cd Mante el día 4 de octubre.
Los saluda
jmd
Inicia Olimpiada de Matemáticas en Tamaulipas
Ya está por iniciarse el proceso de selección para la olimpiada de matemáticas en Tamaulipas. Tentativamente (la convocatoria está por aparecer), las fechas son:
--Etapa municipal, 20 de septiembre.
--Etapa estatal, 27 de septiembre.
Orlando Ochoa Castillo envió a la Delegación Tamaulipas de la OMM un material de entrenamiento para los adolescentes tamaulipecos que se preparan para el concurso estatal (y municipal). Las gracias le sean dadas.
Problema de álgebra --realmente difícil
Calcular la medida de los catetos $a,b$ de un triángulo rectángulo de área 4 e hipotenusa $\sqrt{27}$.
Triminios en un tablero de 2013x2013!!!
En un tablero de 2013 × 2013 se han coloreado k casillas de negro y las demás de blanco, de tal manera que no hay tres casillas negras formando un trimino en ”L”y que al pintar cualquier otra casilla de negro se forma un trimino en ”L” de puras ca
México entra al top 20 en la IMO 2013
Tarde pero sin sueño --como dicen en Viento Libre--, la noticia es que los mexicanos entraron este año 2013 al top 20 (con 3 platas y 3 bronces) en la Olimpiada Internacional de Matemáticas (IMO, por sus siglas en inglés).
La IMO se celebró del 18 al 28 de julio en Santa Marta, Colombia, uno de los mejores lugares turísticos del Caribe colombiano (según la Wikipedia).
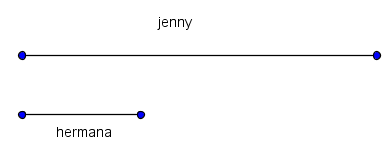
Método Singapur --para razonar problemas verbales elementales
Llamo problemas verbales (word problems) a los problemas razonados con los que se introduce (o debería introducirse) el razonamiento matemático en la escuela primaria (en quinto y sexto año por lo menos). Voy a ilustrar el tema con
Un ejemplo
Jenny tiene 7 pesos y su hermana 2. Después de que su madre les da una misma cantidad de pesos Jenny tiene el doble que su hermana. ¿Cuánto recibieron de su madre?
Solución algebraica