Publicaciones Recientes
ORO para México --en la IMO 2012
Felicidades para la delegación mexicana. Y obviamente para Diego.
Los saluda
jmd

IMO 2012 (día 2)
4. Hallar todas las funciones f:Z→Z que cumplen la siguiente igualdad:
f(a)2+f(b)2+f(c)2=2f(a)f(b)+2f(b)f(c)+2f(c)f(a).
para todos los enteros a,b,c que satisfacen a+b+c=0
(Z denota el conjunto de los números enteros.)
5. Sea ABC un triángulo tal que ∠BCA=90, y sea D el pie de la altura desde C. Sea X un punto interior del segmento CD. Sea K el punto del segmento AX tal que BK=BC. Análogamente, sea L el punto del segmento BX tal que AL=AC. Sea M el punto de intersección de AL y BK. Demostrar que MK=ML
6. Hallar todos los enteros positivos n para los cuales existen enteros no negativos a1,a2…,an tales que
Los problemas de la IMO 2012 (primer día) --Mar del Plata, Arg.
1. Dado el triángulo ABC, el punto J es el centro del excírculo opuesto al vértice A. Este excírculo es tangente al lado BC en M, y a las rectas AB y AC en K y L, respectivamente. Las rectas LM y BJ se intersecan en F, y las rectas KM y CJ se intersecan en G. Sea S el punto de intersección de las rectas AF y BC. Demostrar que M es el punto medio de ST.
2. Si los reales positivos a2,a3,…,an satisfacen a2⋅a3⋯an=1, demostrar que
(a2+1)2(a3+1)3⋯(an+1)n>nn
3. El juego de la adivinanza del mentiroso es un juego para dos jugadores A,B. Las reglas del juego dependen de dos enteros positivos k,n, los cuales son conocidos para ambos jugadores.
Discusión sobre un problema de geometría
En este post voy a tratar de ilustrar, a través de un problema de geometría, la tesis de que la competencia experta en el problem solving requiere de una combinación de técnicas y conocimiento conceptual (de competencias conceptuales pero también procedimentales).
Un problema no trivial de geometría
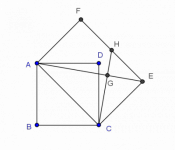
Tomando como base la diagonal AC de un cuadrado ABCD, se construye un rectángulo ACEF de altura el lado del cuadrado y con D dentro de él.
Si H es el punto medio de EF y G es la intersección de AE con CH, demostrar que
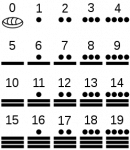
Los sistemas de numeración y los números binarios
Los sistemas de numeración son símbolos y reglas para denotar cantidades Muchas civilizaciones inventaron los suyos, por ejemplo, los romanos usaron la notación I, II, III, IV, .. etcétera.
En nuestros tiempos, el sistema de numeración que usamos cotidianamente se llama sistema de numeración posicional en base 10 (o simplemente sistema decimal). Es decimal pues se usan diez símbolos (a saber 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) y depende de la posición pues no es lo mismo 12 (uno dos) que 21 (dos uno).
La ley de Murphy en ENLACE 2012
En el siguiente post voy a comentar algunas leyes de Murphy relacionadas con la pregunta 92 de ENLACE 2012 (3o Sec.), la cual es de plano una metida de pata extrema de los diseñadores de las preguntas.

Cinco problemas equivalentes al de Fibonacci
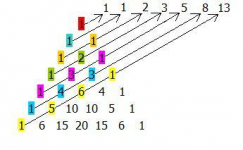
Voy a plantear en este post cinco problemas de combinatoria que son equivalentes al problema de los conejos de Fibonacci, en el sentido de que dan lugar a la misma sucesión (y a la misma recurrencia). La solución de cada uno de ellos se detiene en el modelo, es decir, en el razonamiento por recurrencia que conduce a plantearlo.
1. Subconjuntos sin consecutivos
¿De cuántas formas se puede elegir un subconjunto de {1,2,…,n} de manera que no contenga números consecutivos?
Solución
Problemas de un examen estatal de OMM Jalisco
Sucesiones, recursividad y diferencias finitas
En este post voy a abordar de nuevo el tema de la recursividad a través de algunas sucesiones definidas de manera recursiva. Puesto que la recursión es un tipo de razonamiento muy útil en el problem solving de combinatoria, voy a plantear primero algunos ejemplos de modelación, un tema que se omite en la mayoría de los textos sobre el tema.

Competencia entre 7 jugadores!!!
Se quiere diseñar una competencia entre 7 jugadores de tal manera que de cualquier colección de 3 de ellos al menos dos compitan entre sí. ¿Cuál es el mínimo número de juegos con el que se puede lograr esta condición?
