Publicaciones Recientes
Problema 1 OMM 2003
Problema 1. Dado un número $k$ de dos o más cifras, se forma otro
entero $m$ insertando un cero entre las cifras de las unidades y
de las decenas de $k$. Encuentra todos los números $k$ para los
cuales $m$ resulta ser un múltiplo de $k$.
Cuadrados en cada lado y concurrencia.
Sobre los lados del triángulo ABC se han dibujado los cuadrados $ \mathcal{C}_A $, $ \mathcal{C}_B $ y $ \mathcal{C}_C $, de tal manera que un lado del cuadrado es un lado del triángulo y el cuadrado no traslapa al triángulo. El cuadrado $ \mathcal{C}_A $ se encuentra sobre BC; $ \mathcal{C}_B $ sobre AC; y $ \mathcal{C}_C $ sobre AB.
Problema de cíclicos
En un triángulo acutángulo, el círculo de diámetro AB intersecta la altura CE y su extensión en M y N, y el círculo de diámetro AC intersecta la altura BD y su extensión en P y Q. Probar que los puntos M, N, P, Q están sobre una misma circunferencia.
(Nota:Este problema es una extensión del problema dos segmentos iguales.)
Rectas notables del triángulo
Éstas son las rectas notables del triángulo
En el siguiente interactivo se muestran las rectas notables del triángulo. Selecciona cuál recta quieres ver y observa la definición y la figura. No olvides descargar la versión imprimible de este acordón de rectas notables.
Criterios de Divisibilidad
Criterios de divisibilidad más comunes y útiles en concursos de matemáticas.
| entre $n$ | criterio | comentario |
| $2$ | dígito de unidades par | recuerda que el cero es par |
| $3$ | suma de dígitos es múltiplo de $3$ | muy útil en concursos |
| $4$ | últimos dos dígitos múltiplo de $4$ | $284, 84=4(21)$ |
Tutorial básico: Construcción de figuras geométricas con Geogebra. Parte 3.
NOTA: Este tutorial te servirá para en aprender a usar el software o herramienta GeoGebra. Si lo que buscas es cómo hacer construcciones geométricas, te recomendamos que estudies el libro en línea de MaTeTaM llamado Construcciones geométricas con regla y compás. Es un libro interactivo que te mostrará como realizar construcciones geométricas paso a paso.
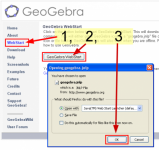
En la parte 2 de este tutorial vimos un ejemplo paso a paso para hacer una construcción geométrica en GeoGebra. Ahora aprenderás cómo exportar ese dibujo a formato PNG y cómo hacer un applet a partir de tu construcción.
Tutorial básico: Construcción de figuras geométricas con Geogebra. Parte 2.
NOTA: Este tutorial te servirá para en aprender a usar el software o herramienta GeoGebra. Si lo que buscas es cómo hacer construcciones geométricas, te recomendamos que estudies el libro en línea de MaTeTaM llamado Construcciones geométricas con regla y compás. Es un libro interactivo que te mostrará como realizar construcciones geométricas paso a paso.
En la primera parte de este tutorial se hizo un vistazo rápido de GeoGebra, aquí veremos un ejemplo que te guiará paso a paso a construir un triángulo y su circuncírculo.
1. Haz clic en el icono y dibuja 3 puntos en el área gráfica.
2. Haz clic en el icono . Para hacer el segmento AB sólo hay que hacer clic primero en el punto A y luego en el punto B. De la misma forma hacer BC y AC.

Tutorial básico: Construcción de figuras geométricas con Geogebra. Parte 1.
NOTA: Este tutorial te servirá para en aprender a usar el software o herramienta GeoGebra. Si lo que buscas es cómo hacer construcciones geométricas, te recomendamos que estudies el libro en línea de MaTeTaM llamado Construcciones geométricas con regla y compás. Es un libro interactivo que te mostrará como realizar construcciones geométricas paso a paso.
Bisectriz, ángulo recto y conjugados armónicos
Consideremos P y Q un par de puntos conjugados armónicos con respecto a A y B, P dentro d
Problema de Excalibur Probleam Corner 309
En un triángulo acutángulo ABC donde AB < AC. Sea H el pie de la perpendicular de A sobre BC y M el punto medio de AH. Sea D el punto de tangencia del incirculo del triangulo ABC en BC. La linea DM intersecta por segunda vez al incirculo en N. Probar que los angulos BND y CND son iguales.
