Publicaciones Recientes
Argumentos básicos de conteo 5 (Funciones Generatrices)
Cuadrilátero cícliclo dentro de un cuadrilátero circunscrito
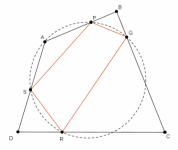
Sea ABCD un cuadrilátero para el cuál existen cuatro puntos P, Q, R y S sobre los lados AB, BC, CD y DA respectivamente y tales que PB=BQ, QC = CR, RD = DS y SA = AP. Demuestra que:
- a) El cuadrilátero ABCD es circunscrito
- b) El cuadrilátero PQRS es cíclico.
Problema 4 OIM 1997
Sea n un entero positivo. Consideremos la suma $x_1y_1 + x_2y_2 + \ldots + x_ny_n$, donde los valores que pueden tomar las variables $x_1, x_2, \ldots, x_n, y_1, y_2, \ldots, y_n$ son únicamente 0 y 1. Sea $I(n)$ el número de $2n$-adas $(x_1, x_2, \ldots, x_n, y_1, y_2, \ldots, y_n)$ para las cuales el valor de la suma es un número impar y sea $P(n)$ el número de $2n$-adas $(x_1, x_2, \ldots, x_n, y_1, y_2, \ldots, y_n)$ para las cuales la suma toma valor par. Probar que
$$\frac{P(n)}{ I(n)}=\frac{2^n + 1}{2^n - 1}$$
IMO 2009, Problema 5
Determinar todas las funciones f del conjunto de los enteros positivos en el conjunto de los enteros positivos tales que, para todos los enteros positivos a y b, existe un triángulo no degenerado cuyos lados miden
$$a, f(b) \textrm{ y } f(b + f(a) - 1)$$
(Un triángulo es no degenerado si sus vértices no están alineados).
P1. OMM 1988. Siete pelotas blancas y cinco negras
¿De cuántas formas se pueden acomodar en línea recta siete pelotas blancas y cinco negras, de tal manera que no estén dos pelotas negras juntas?
Argumentos básicos de conteo 4 (Combinaciones 2a parte)
Argumentos básicos de conteo 3 (Combinaciones)
Intro
En este post vamos a derivar la fórmula para las combinaciones de n objetos tomados de r en r. Así se decía antes, ahora se prefiere decir el número de subconjuntos de tamaño r tomados de un conjunto de tamaño n. De nuevo, aquí lo importante es el razonamiento combinatorio que da lugar a la fórmula.
IMO4_2009_invertido
Sean ABC un triángulo isósceles rectángulo en A, J su incentro y AD, BE las bisectrices de los ángulos A y B, respectivamente. La altura AD es tangente al incírculo del triángulo ADC (con incentro en I) en P y al lado CA en Q. Demostrar que:
Argumentos básicos de conteo 2 (r-listas)
Argumentos básicos de conteo
Con este post estoy inaugurando una sucesión que podría llegar hasta 20. La idea es la misma que la que usé con los GBC-teoremas, es decir, formular una serie de hechos básicos sobre el tema. En los teoremas de geometría básica del círculo me vi limitado por el formato de teorema y no añadí comentarios u otras ayudas didácticas. Es por eso que ahora, para los hechos básicos de combinatoria, elijo la entrada de blog para difundir es conocimiento básico, dada la flexibilidad de su formato.
