IMO 2009
IMO 2009, Problema 5
Determinar todas las funciones f del conjunto de los enteros positivos en el conjunto de los enteros positivos tales que, para todos los enteros positivos a y b, existe un triángulo no degenerado cuyos lados miden
a,f(b) y f(b+f(a)−1)
(Un triángulo es no degenerado si sus vértices no están alineados).
IMO 2009, Problema 3
Sea s1,s2,s3,… una sucesión estrictamente creciente de enteros positivos tal que las
subsucesiones
ss1,ss2,ss3,… y ss1+1,ss2+1,ss3+1,…
son ambas progresiones aritméticas. Demostrar que la sucesión s1,s2,s3,... es también una progresión
IMO 2009 Problema 1
Sea n un entero positivo y sean a1,a2,...,ak(k≥2) enteros distintos del conjunto 1,...,n, tales que n divide a ai(ai+1−1), para i=1,...,k−1. Demostrar que n no divide a ak(a1−1).
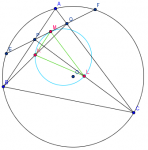
IMO 2009 Problema 2
Sean ABC un triángulo de circuncentro O, P y Q puntos sobre AB y AC, respectivamente, y K, L, M los puntos medios de BQ, CP y PQ, respectivamente. Si el circuncírculo del triangulo KLM es tangente a PQ, demostrar que OP=OQ.
IMO 2009 Problema 4
En un triángulo ABC, donde AB=AC, los bisectrices internas de ∠A y ∠B cortan a los lados BC y AC en D y E, respectivamente. Sea I el incentro del triángulo ADC. Supongamos que ∠IEB=45. Encontrar todos los valores posibles de ∠A.

