Publicaciones Recientes
¿Dónde y cómo aprender ecuaciones funcionales?
Bueno como dice el título, necesito aprender ecuaciones funcionales para la olimpíada. Busqué en internet apuntes pero todos son complejos y yo necesito algo gradual que empiece desde lo básico, ya que no dispongo de nadie que me explique. Principalmente necesitaría que me digan los conocimientos previos que necesito para aprender el tema, ya que no sé absolutamente nada de funciones, sólo lo básico. Cualquier recomendación de libros o apuntes me vendría de maravillas.
Dede ya muchas gracias y espero con ansias sus respuestas.
Ranas, hormigas, camaleones...
Después de escribir el post sobre paridad estuve navegando la Web con el tema invariantes, otro tipo de razonamiento en el problem solving de olimpiada que generalmente acompaña al de paridad.

Argumento de paridad: tres instancias de uso
Voy a discutir en este post un razonamiento elemental en el campo de las matemáticas de concurso denominado argumento de paridad. Es recurrente en el problem solving de olimpiada. Se presentan las propiedades básicas de la paridad y algunas instancias de uso.
Discusión previa
Así como las personas pueden ser clasificados por su sexo (femenino/masculino), los números enteros se pueden clasificar por su paridad (par, impar).
La paridad de un entero es así una variable dicotómica: el número es par o bien no lo es (en cuyo caso se le llama impar o non). Una clasificación elemental... pero tiene sus detalles finos (esa verdad no está en los libros, sino en sus instancias de uso).
Una propiedad elemental de la divisibilidad
Voy a discutir en este post una propiedad de la divisibilidad que surge cuando la suma de dos números es múltiplo de un primo. Se le podría llamar propiedad de transferencia de la divisibilidad. Incluyo dos instancias de uso en el problem solving de olimpiada.
Una propiedad de transferencia
Considere la suma $a+b$ de dos números enteros y supongamos que es múltiplo de un primo $p$. Puede suceder que ninguno de los sumandos sea múltiplo de $p$. Pero si alguno lo es, entonces también lo es el otro. Formalmente, la propiedad se puede establecer así:
$a,b\in\mathbb{Z},p$ primo, $p|a+b\Rightarrow (p|a\Leftrightarrow p|b)$
Numeros aluxes
Un entero positivo $n$ es aluxe si el producto de los digitos de $n$ es igual al producto de los digitos de $n+1$. ¿Cuántos enteros aluxes hay menores o iguales a 2011 y mayores o iguales a 1?
Principio de sustitución
Si dos cantidades son iguales entonces son intercambiables --en el cálculo o demostración.
Parece trivial. Y lo es. Pero hay que aprender a usarlo. Antiguamente se solía decir:
Dos cosas iguales a una tercera son iguales entre sí.
Pero no se trata de aprender a recitarlo, se trata de aprender a usarlo.
Ejemplos:
1. Considere el sistema $x+y=z$, $z=5$
Aquí tenemos que (dos cosas) $x+y$ y 5 son iguales a $z$ (una tercera). Por tanto, $x+y=5$ (son iguales entre sí).
Discusión sobre las coordenadas de un punto
División sintética --cálculo numérico de $P(x)/(x-c)$
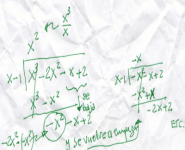
División larga: un algoritmo muy fácil de ignorar
Iba a poner un post sobre división sintética. Lo pospuse para el siguiente. Pues ese algoritmo requiere saber los rudimentos de la división larga. Así que me entretuve (trasquilé la borrega) averiguando cómo se hace (si es que se hace) para enseñar la división larga en la primaria. Y el resultado es este post sobre la división larga. Pues tengo la sospecha (que no carece de evidencia) de que más de la mitad de los alumnos de secundaria no manejan ese algoritmo --mi evidencia son mis alumnos en la universidad...

Examenes de la Olimpiada Iberoamericana de Matemáticas por fin en MaTeTaM
Ya habíamos agregado todos los exámenes de las Olimpiada Mexicana de Matemáticas, ahora por fin tenemos todos los exámenes de la Olimpiada Iberoamericana de Matemáticas.

