Publicaciones Recientes
2.- Ataque de torres en un tablero cúbico.
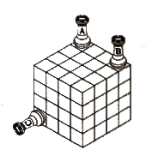
Sea n un entero positivo. David tiene 6 tableros de ajedrez de n×n que ha dispuesto de manera que formen las 6 caras de un cubo de n×n×n. Se dice que dos casillas a y b de este nuevo tablero cúbico están alineadas si podemos conectarlas por medio de un camino de casillas a=c1,c2,…,cm=b de manera que cada pareja de casillas consecutivas en el camino comparten un lado, y los lados que la casilla ci comparte con sus vecinas son lados opuestos del cuadrado ci, para i=2,3,…,m−1. Diremos que dos torres colocadas sobre el tablero se atacan; si las casillas que ocupan están alineadas. David coloca algunas torres sobre el tablero de forma que ninguna ataque a otra.
1.- Números Tlahuicas
Un número x es Tlahuica si existen números primos distintos p1,p2…,pk tales que
x=1p1+1p2+...+1pkDetermina el mayor número Tlahuica que satisface las dos propiedades siguientes:
- 0 < x < 1
- existe un número entero 0<m≤2022 tal que mx es un entero.
El 6 del último selectivo 2022
Se definen las sucesiones xn y yn mediante las siguientes reglas:
- x0 = 2, x1 = 5, xn+1 = xn + 2xn-1
- y0 = 3, y1 = 4, yn+1 = yn + 2yn-1
Demuestra que no hay números que estén en ambas sucesiones.
Sin miedo al factorial
Determina el menor entero positivo n tal que para todo entero positivo u se cumple que n + u! sea un número de al menos 4 divisores
Isósceles en 2 circunferencias de mismo radio
Sean α y β dos circunferencias con el mismo radio. Dichas circunferencias se intersectan en puntos P y Q. Sea X un punto en α. La recta QX intersecta a β en un punto Z, de manera que Z queda entre X y Q. Demuestra que PX=PZ.
Paralelogramo con solo 3 vértices en una circunferencia
Sea ABCD un paralelogramo. Sean K y L las intersecciones del circuncírculo de ABC con los lados AD y CD respectivamente. Sea M el punto medio del arco KL que no contiene a B. Demuestra que DM es perpendicular a AC.
Múltiplos de 9 con restricciones
¿Cuántos múltiplos de 9 menores que 1000 no usan ningún digito menor que 3?
Promedio de un colección de m números
a) Demuestra que si a una colección de m números le agregamos su promedio, la nueva colección de m+1 números tendrá el mismo promedio.
b) Demuestra que el promedio de una colección de m números es menor o igual a su número más grande, y mayor o igual a su número más pequeño.
El 6 del estatal 2022
En una circunferencia Γ con centro en D se trazan dos tangentes AE y AF con E y F sobre Γ. Sean B y C puntos sobre los segmentos AE y AF respectivamente de tal manera que BC también es tangente a Γ. Sea J la intersección de BD con EF. Demuestra que el ángulo CJB es un ángulo recto.
Problema 5 Estatal 2022
Encuentra todas las parejas de enteros positivos (x,n) tales que:
(3)(2x) + 4 = n2
