Publicaciones Recientes
Otra forma de ver Cauchy
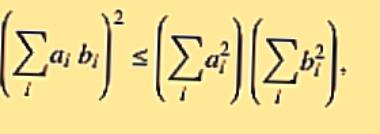
Resultados parciales de la selección Tamaulipas
Problema 1 Problema 2 Problema 3 Problema 4 Problema 5 Proble
Noticias de Campeche
Como ya se dieron cuenta ya están en MaTeTaM los problemas del concurso nacional de la Olimpiada Mexicana de Matemáticas en su versión 2009. Según comunicado de Ramón el examen estuvo muy difícil (en opinión generalizada) y tenemos los siguientes pronósticos:
--Casanova, mención :(
XXIIIOMM Problema 6
En una fiesta con n personas se sabe que de entre cualesquiera 4 personas, hay 3 de las 4 que se conocen entre sí o hay 3 que no se conocen entre sí. Muestra que las n personas se pueden separar en 2 salones de manera que en un salón todos se conocen entre sí y en el otro salón no hay dos personas que se conozcan entre sí.
XXIIIOMM Problema 5
Considera un triángulo ABC y un punto M sobre el lado BC. Sea P la intersección de las perpendiculares a AB por M y a BC por B, y sea Q la intersección de las perpendiculares a AC por M y a BC por C. Muestra que PQ es perpendicular a AM si y sólo si M es punto medio de BC.
XXIIIOMM Problema 4
Sea n>1 un entero impar y sean a1,a2,…,an números reales distintos. Sea M el mayor de estos números y sea m el menor de ellos. Muestra que es posible escoger los signos de la expresión s=±a1±a2±…±an de manera que m<s<M.
XXIIIOMM Problema 3
Sean a,b,c números reales positivos tales que abc=1. Muestra que
a3a3+2+b3b3+2+c3c3+2≥1 y que 1a3+2+1b3+2+1c3+2≤1
XXIIIOMM Problema 2
En cajas marcadas con los números 0,1,2,3,... se van a colocar todos los enteros positivos de acuerdo con las siguientes reglas:
XXIIIOMM Problema 1
Sean ABC un triángulo y AD la altura sobre el lado BC. Tomando a D como centro y a AD como radio, se traza una circunferencia que corta a la recta AB en P, y corta a la recta AC en Q. Muestra que el triángulo AQP es semejante al triángulo ABC.
Si no se puede expresar, lo mejor es callar
¿Alguien se ha dado cuenta de que es necesario censurar y editar nuestro lenguaje? Quiero decir, ante el riesgo de interpretaciones equivocadas en términos de ecología, de género, de protección a los animales, etc. Por ejemplo, tomemos el caso de los modos femeninos de interpretar y procesar la información.
