Publicaciones Recientes
Problema 3
De http://www.arrakis.es/, un sitio muy recomendable para los aficionados a las matemáticas de concurso --y que no anden ya en las internacionales— tomo el
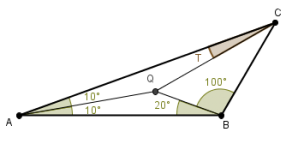
Problema 3.Un triángulo ABC tiene en su interior un punto Q de tal manera que los ángulos en la base AB del ABQ son 10 y 20, en la base BC de BCQ son 100 y X, y en la base CA de CAQ son de T y 10. Encontrar T.
Problema 2
Del libro de R. Bulajich y J.A. Gómez Ortega (Geometría)y que llevé ese primer día al taller elegí el
Problema 2.Sobre los lados AB y AC del triángulo ABC se construyen los equiláteros ABC’ y ACB’, los segmentos BB’ y CC’ son iguales. Demostrarlo.
Comentarios previos:
El problema es clásico, y es elemental pero difícil. Lo que me gustaría comentar antes de continuar con la solución es que la configuración clave (que “hace la luz” y que permite avanzar hacia la solución) hay que aislarla de la figura completa.

Problema 1
Los chicos sacaron su cuaderno y me plantearon el
Problema 1:En el triángulo ABC, con ángulo recto en B, los puntos E y F están en AC de tal manera que AE=AB y CF=CB. ¿Cuánto mide el ángulo EBF?
Solución:
(Decidí aceptar el reto de resolver (ayudar a resolver) este problema elemental de geometría que tiene sin embargo sus detalles finos. Empecé con una discusión sobre dibujar la figura y evocar significados teóricos a partir de los datos.)

Los problemas
Presento entonces los cuatro problemas que discutimos en el taller junto con sus soluciones, todas ellas con congruencia de triángulos.
Geometría básica para principiantes
Este libro aun continua en desarrollo, está pensado para estudiantes que se inician en el estudio de la geometría de olimpiadas, los primeros capítulos incluso pueden ayudar a los estudiantes que sólo desean mejorar o complementar sus conocimientos de geometría escolarizada (secundaria o bachillerato).
Solución de congruencias potenciales
Sea a un entero positivo, coprimo con un primo p. Analizar la ecuación de congruencias xn≡a(modp) en cuanto a sus posibles soluciones.
Sobre la noción de congruencia de triángulos
A lo largo de este capitulo veremos la definición de congruencia y algunos usos prácticos en la argumentación para la solución de problemas.
La congruencia no la definiremos formalmente si no hasta la sección "Congruencia de triángulos como noción intuitiva y su formalización".
Raíces primitivas de un primo: una propiedad logarítmica
Sean p un número primo y g una de sus raíces primitivas. Demostrar que dos enteros positivos i,j son equiresiduales en la división entre p−1 si y sólo si gi,gj son equiresiduales en la división entre p
Un punto en el interior de un triángulo
Sean P un punto en el interior del triángulo ABC y un ángulo α dado. Los ángulos en la base AB del triángulo ABP miden x y 90−2α, los ángulos en la base BC del triángulo BCP miden 90−2α y 2α−60, y los de la base CA del triángulo CAP miden 60+α y T. Encontrar el valor de x en términos de α. (¿Qué condiciones debe cumplir el valor α.)
Isósceles y equilátero --elemental pero no trivial
Sean ABC un triángulo, con AB=AC y ángulo en A de 100 grados, y un punto B' en el mismo plano de tal manera que AB'C es equilátero. Encontrar el ángulo ABB'.
