Publicaciones Recientes
Selección Tamaulipas para la XXVI OMM
Un poco tarde pero aquí está la selección que acudirá al concurso nacional de la Olimpiada Mexicana de Matemáticas el próximo mes de noviembre.
Claudia Lorena Cabrera Arjona
Oscar Gilberto Brewer De la Vega
Eduardo Alexis Romo Almazán
Emmanuel Sanchez Sandoval
Gerardo Cantú González
Mariano Narváez Pozos
Sacnicté
De vez en cuando se encuentra uno con verdaderos talentos adolescentes dentro del campo de las matemáticas escolares.
Se puede decir que todos los adolescentes son iguales (tienen las mismas capacidades intelectuales). Sólo que "algunos son más iguales que otros" (para usar la famosa frase de George Orwell en la novela satírica denominada Rebelión en la Granja --Animal Farm).
Sacnicté: veni, vidi, vici
Sacnicté, la niña del COBAT 06 (de Ocampo), quien resolvió correctamente tres de los 4 problemas del concurso estatal de la OMM Tamaulipas 2012, es igual que todos los 102 participantes en ese concurso... sólo que es un poquito más igual que ellos.
Preselección OMM Tamaulipas 2012
He aquí la lista de la preselección OMM Tamaulipas 2012 (tal y como me la envió el delegado Ramón Jardiel Llanos Portales --así que cualquier aclaración, felicitación o incluso impugnación, sea ésta con pruebas o sin pruebas, por favor comunicarla directamente a rjardiel5@hotmail.com ).
|
GABRIELA SAC-NITE GUEVARA MTZ |
OMM Tamaulipas 2012: concurso estatal
El día de hoy, 5 de octubre, se aplicó el concurso estatal en las instalaciones de la UAMCEH-UAT, de donde resultó una preselección compuesta por 26 adolescentes aficionados a las matemáticas (de nuestro sistema educativo tamaulipeco). Enseguida se presentan los 4 problemas del examen (con sus soluciones) y, al final se añaden algunos comentarios sobre los problemas y los resultados del concurso.
Los problemas
1A. Factorizar la ecuación cuadrática 2011x2+2012x+1=0.
Solución
Es fácil darse cuenta que una de sus raíces es -1 (dado que la satisface). Y dividiendo entre x+1 se obtiene que la ecuación se factoriza como
Los problemas de la XXVII OIM (Cochabamba 2012)
Como se sabe, la Olimpiada Iberoamericana de Matemáticas se realizó esta semana en Cochabamba. Enseguida presento los problemas tomados del facebook de la OMM (de una comunicación de Amanda Rhoton).
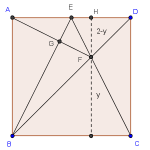
Equiláteros en un rectángulo
Concurso ciudades OMM Tamaulipas 2012: soluciones
Concurso ciudades XXVI OMM Tamaulipas 2012
A continuación se presentan los problemas del concurso ciudades con que inició --el viernes 21 de septiembre-- el proceso de selección Tamaulipas 2012 para la XXVI Olimpiada Mexicana de Matemáticas --cuyo concurso nacional se realizará en noviembre en Guanajuato. Se añaden algunos comentarios de parte del que esto escribe --a partir de los enunciados y de las soluciones presentadas por los concursantes...
Los problemas
1G. En el segmento AB se elige un punto E. En los extremos de AB se levantan dos segmentos AD y BC, perpendiculares a AB, de tal manera que AD=AE y BC=BE. Demostrar que el triángulo CDE es rectángulo en E.
Problema clásico de seccionado
Sea ABCD un cuadrilátero convexo. Encontrar un punto M en BC (mostrar el procedimiento con prueba) de tal manera que AM divida al cuadrilátero ABCD en dos regiones de igual área.
Comparación indirecta de dos ángulos
Sea ABC un triángulo isósceles rectángulo en C. Si D es el punto medio de BC y la perpendicular a AD por C corta a AB en E, demostrar que los ángulos ADC y EDB tienen la misma medida.
Ejercicio en congruencia de triángulos
Dado el triángulo isósceles ABC, con AB=AC,sean D un punto en AB y E otro punto en la extensión de AC de tal manera que BD=CE. Si G es el punto de intersección de DE con BC, demostrar que DG=GE.
