Publicaciones Recientes
Teoremas de la línea media
El segmento que une los puntos medios de dos lados de un triángulo es paralelo al tercero y mide la mitad de éste.
Este es un teorema muy útil en la solución de problemas geométricos. De hecho se trata de dos teoremas de la línea media (el otro dice: paralela a la base por punto medio pasa por el punto medio) y pueden ser demostrados usando trazos auxiliares para formar triángulos congruentes.
Segunda instancia de uso del criterio LAL
En un triángulo isósceles, la bisectriz del ángulo opuesto a la base divide al triángulo en dos congruentes.
Demostración:
En la figura de arriba trácese la bisectriz del ángulo C y suponga que corta al lado AB en M. Por hipótesis los ángulos ACM y MCB son iguales. Esto sugiere la correspondencia C-C. Por otro lado, también por hipótesis, AC=CB. Esto sugiere la correspondencia A-B, y el otro punto común a los triángulos formados por la bisectriz es M, lo cual sugiere la correspondencia M-M.
Teorema del triángulo isósceles
Advertencia: Esta instancia de uso es algo desconcertante cuando se ve por primera vez, así que se pide la cooperación cognitiva del lector. (El desconcierto se debe quizá a que el triángulo se pone en correspondencia consigo mismo, lo cual no está prohibido pero como que uno piensa que esa prohibición quedaba implícita en la definición de congruencia.)
Si un triángulo es isósceles entonces sus ángulos en la base son iguales. (Nota: se acostumbra entender por base, el tercer lado –los dos primeros son los que sabemos iguales.)

Instancias de uso clásicas del criterio LAL
Mostraremos ahora algunos problemas ejemplo donde resulta útil el criterio de congruencia LAL. Se le invita al lector a intentar primero resolver los ejercicio planteados y posteriormente leer la solución propuesta.
Criterios de congruencia como postulados
Los criterios o principios de congruencia nos dicen cómo determinar si dos triángulos son congruentes sin necesidad de verificar las seis igualdades entre lados y ángulos correspondientes.
Criterio LAL (Lado-ángulo-lado). Es posiblemente el criterio de congruencia más básico, este criterio nos dice que si, en una correspondencia de triángulos, dos lados de uno y el ángulo comprendido entre ellos son iguales a sus correspondientes elementos en el otro, entonces los dos triángulos son congruentes.
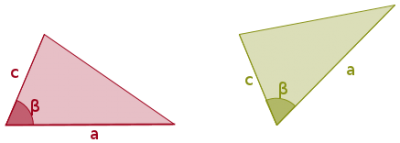
Congruencia de triángulos como noción intuitiva y su formalización
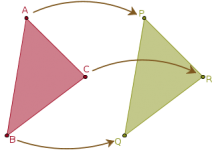
Después de haber descubierto el hecho de que dos triángulos son congruentes (iguales) es conveniente poner sus vértices en correspondencia.

El triángulo como configuración de puntos y rectas
Como se sabe, hay diversas clasificaciones de triángulos que dan cuenta de su diversidad de forma: de acuerdo a la medida de sus ángulos pueden ser obtusángulos, rectángulos, acutángulos; de acuerdo a la relación de las medidas de sus lados pueden ser equiláteros, isósceles, escalenos. Es por eso que una noción previa a la definición de congruencia de triángulos es la de corres
Igualdad y congruencia
El concepto de congruencia está emparentado con el de igualdad y se espera que el aprendiz la conozca ya sea por su significado intuitivo a partir del lenguaje natural, o bien a través de su uso en la aritmética.
Es costumbre que en geometría se hable de congruencia en vez de igualdad. Por ejemplo dos segmentos son congruentes si y sólo si tienen la misma medida –y lo mismo es cierto para ángulos. Pero en el caso de dos triángulos la definición es más complicada pues no hay una medida (número) que defina a un triángulo.

Uno de cuadráticas
El cuadrado de un número disminuido en 924 es igual 20 veces dicho número. ¿Cuál es ese número? (Genera uno similar.)
Dos en uno
La suma de dos números es 36 (variante: 750) y su producto es 243 (variante: 78125). Encuentra los números. ¿Podrías plantear uno con la misma estructura?
