Publicaciones Recientes
P4 OMM 2005. Eliminar (ternas aritméticas) reordenando
Decimos que una lista de números a1,a2,…,am contiene una terna aritmética ai,aj,ak, si i<j<k y 2aj=ai+ak. Por ejemplo, 8,1,5,2,7 tiene una terna aritmética (8,5 y 2) pero 8,1,2,5,7 no. Sea n un entero positivo. Muestra que los números 1,2,…,n se pueden reordenar en una lista que no contenga ternas aritméticas.
P5 OMM 2005. Con cualquiera de las restantes se completa
Sea N un entero mayor que 1. En cierta baraja de N3 cartas, cada carta está pintada de uno de N colores distintos, tiene dibujada una de N posibles figuras y tiene escrito un número entero del 1 al N (no hay dos cartas idénticas). Una colección de cartas de la baraja se llama completa si tiene cartas de todos los colores, o si entre sus cartas aparecen todas la figuras o todos los números. ¿Cuántas colecciones no completas tienen la propiedad de que, al añadir cualquier otra carta de la baraja, ya se vuelven completas?
P3 OMM 2005. Infinidad de enteros en sucesión de fracciones
Determina todas las parejas (a,b) de enteros distintos de cero para las cuales es posible encontrar un entero positivo x primo relativo con b y un entero cualquiera y, tales que en la siguiente lista hay una infinidad de números enteros:
a+xyb,a+xy2b2,a+xy3b3,…,a+xynbn,…
P2 OMM 2005. Matrices n-balanceadas
Dadas varias cuadrículas del mismo tamaño con números escritos en sus casillas, su suma se efectúa casilla por casilla. Por ejemplo:
Dado un entero positivo N, diremos que una cuadrícula es N-balanceada si tiene números enteros escritos en sus casillas y si la diferencia entre los números escritos en cualesquiera dos casillas que comparten un lado es menor o igual que N.

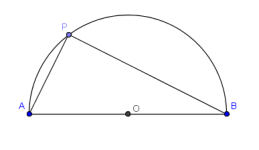
P1 OMM 2005. Circuncírculo en circuncírculo
Sea O el centro de la circunferencia circunscrita al triángulo ABC, y sea P un punto cualquiera sobre el segmento BC (P≠B y P≠C). Supón que la circunferencia circunscrita al triángulo BPO corta al segmento AB en R (R≠A y R≠B) y que la circunferencia circunscrita al triángulo COP corta al segmento CA en el punto Q (Q≠C y Q≠A).
- (i) Considera el triángulo PQR; muestra que es semejante al triángulo ABC y que su ortocentro es O.
- (ii) Muestra que las circunferencias circunscritas a los triángulos BPO,COP y PQR son todas del mismo tamaño.
Inferencias elementales a partir de la congruencia de ángulos
Este post, al igual que el anterior, se inscribe en la Reforma al Bachillerato (Bloque I, Matemáticas II). En él voy a elaborar (discutir) sobre los procesos de inferencia que pueden realizarse en configuraciones geométricas muy básicas, utilizando el concepto de ángulos congruentes. Y algunos resultados muy básicos, como el de la suma de los ángulos interiores de un triángulo, las relaciones de complementariedad y suplementariedad de dos ángulos.
P6 OMM 2004. Cambios de dirección en cuadrícula 2004X2004
¿Cuál es el mayor número posible de cambios de dirección en un recorrido sobre las líneas de una cuadrícula de 2004×2004 casillas, si el recorrido no pasa dos veces por el mismo lugar?
P5 OMM 2004. Dos circunferencias
Sean α y β dos circunferencias tales que el centro O de β está sobre α. Sean C y D los dos puntos de intersección de las circunferencias. Se toman un punto A sobre α y un punto B sobre β tales que AC es tangente a β en C y BC es tangente a α en el mismo punto C. El segmento AB corta de nuevo a β en E y ese mismo segmento corta de nuevo a α en F. La recta CE vuelve a cortar a α en G y la recta CF corta a la recta GD en H. Prueba que el punto de intersección de GO y EH es el centro de la circunferencia circunscrita al triángulo DEF.
P4 OMM 2004. Número de equipos en un torneo
Al final de un torneo de futbol en el que cada par de equipos jugaron entre si exactamente una vez y donde no hubo empates, se observó que para cualesquiera tres equipos A,B,C, si A le ganó a B y B le ganó a C entonces A le ganó a C. Cada equipo calculó la diferencia (positiva) entre el número de partidos que ganó y el número de partidos que perdió. La suma de todas estas diferencias resultó ser 5000. ¿Cuántos equipos participaron en el torneo? Encuentra todas las respuestas posibles.
P3 OMM 2004. Configuración con incírculo y punto medio
Sean Z,Y los puntos de tangencia del incírculo del triángulo ABC con los lados AB,CA, respectivamente. La paralela a YZ por el punto medio M del lado BC, corta a CA en N. Sea L el punto sobre CA tal que NL=AB (y L del mismo lado de N que A). La recta ML corta a AB en K. Muestra que KA=NC.
