Publicaciones Recientes
IMO 2009 Problema 2
Sean ABC un triángulo de circuncentro O, P y Q puntos sobre AB y AC, respectivamente, y K, L, M los puntos medios de BQ, CP y PQ, respectivamente. Si el circuncírculo del triangulo KLM es tangente a PQ, demostrar que OP=OQ.
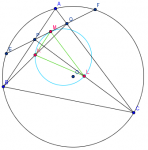
IMO 2009 Problema 4
En un triángulo $ ABC $, donde $AB=AC$, los bisectrices internas de $\angle{A}$ y $\angle{B}$ cortan a los lados $ BC $ y $AC$ en $D$ y $E$, respectivamente. Sea $I$ el incentro del triángulo $ADC$. Supongamos que $\angle{IEB}=45$. Encontrar todos los valores posibles de $\angle{A}$.

Probar isósceles
En una semicircuferenica de diámetro AB se elige un punto D y se baja una perpendicular al diámetro AB cortándolo en C. En el espacio descrito por DC, CB y el arco BD se inscribe un círculo tangente a CD en L, a BC en J y al arco BD en K. Demostrar que AD=AJ.
Encontrar el término n de una sucesión
Considere la sucesión $a_1=1$ y, para $ n $ mayor que 1, $a_n=1+2a_{n-1}.$ Encontrar una fórmula para el término n-ésimo y demostrarla por inducción.
Saltillo 2007
Fotos de la Olimpiada Mexicana de Matemáticas celebrada en saltillo de 2007. Por la selección de tamaulipas.
Potencia de un punto y circunferencias ortogonales
Sean dados una circunferencia c de radio r y centro O, y dos puntos M y M' tales que $OM\cdot OM'=r^2$ (i.e., inversos uno del otro respecto a c). Demostrar que cualquier circunferencia c' que pase por M y M' es ortogonal a c.
Condición necesaria y suficiente para cíclicos
Sea PQRS un cuadrilátero tal que sus lados opuestos PR y QS se cortan en un punto T. Demostrar que PQRS es cuadrilátero cíclico si y sólo si $TR\cdot TP=TS\cdot TQ.$
El lugar geométrico de la reflexión de un punto
Sean $ P$ un punto en el interior de una circunferencia $\mathcal{C}$ y $ M$ un punto sobre $\mathcal{C}$. Definamos $ N$ el punto sobre $\mathcal{C}$ tal que el ángulo $\measuredangle MPN = 90^{\circ}$ (en sentido contrario de las manecillas del reloj). Llamemos $P'$ el punto que resulta de reflejar $ P$ con respecto a $MN$.
Construcción de una circunferencia ortogonal
Sea dada una circunferencia $c$. Demostrar que el siguiente procedimiento produce una circunferencia ortogonal a $c$ con centro en un punto $P$ fuera de $c$.
1) Trazamos las tangentes a $c$ desde $P$ ubicando los puntos de tangencia $T$ y $T'$.
2) Trazamos la circunferencia con centro en $P$ y radio $PT$. Esta es la circunferencia ortogonal pedida.
