Publicaciones Recientes
Desigualdad homogenea
Sean $a, b, c$ números reales positivos que satisfacen $a+b+c = 1$.
Muestra que: $$\sqrt{a + bc} + \sqrt{b + ca} + \sqrt{c + ab}\leq 2.$$
Lugar geométrico equiangular
Dado un triángulo equilátero $ABC$, encuentra todos los puntos $P$ del plano que cumplan $\angle{APB} = \angle{BPC}$.
Diez consecutivos son divisores --pero no 11
Encuentra todos los enteros positivos $N$ con la siguiente propiedad: entre todos los divisores positivos de $N$, hay 10 números consecutivos, pero no 11.
La arista es el MCD de sus vértices
En los vértices de un cubo están escritos 8 enteros positivos distintos, uno
en cada vértice. Y en cada una de las aristas está escrito el máximo común
divisor de los números que están en los 2 vértices que la forman. Sean $A$ la suma de los números escritos en las aristas y $V$ la suma de los números escritos en los vértices.
- (a) Muestra que $\frac{2}{3}A\leq V$.
- (b) ¿Es posible que $A = V$?
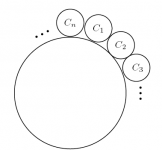
Juego de caballeros
Los caballeros $C_1,C_2,\ldots,C_n$, del Rey Arturo, se sientan en una mesa
redonda de la siguiente manera:
El rey decide realizar un juego para premiar a uno de sus caballeros. Iniciando con $C_1$, y avanzando en el sentido de las manecillas del reloj, los caballeros irán diciendo los números 1, 2, 3, luego 1, 2, 3, y así sucesivamente (cada caballero dice un número). Cada caballero que diga 2 ó 3 se levanta inmediatamente y el juego continúa hasta que queda un solo caballero: el ganador.
Caballos en el tablero
Considera un tablero de ajedrez. Los números del 1 al 64 se escriben en las casillas del tablero como en la figura:
1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
Expresado como suma de potencias --de sus primeros dos divisores
Sean $1=d_1 < d_2 < d_3 \cdots < d_k = n$ los divisores del entero positivo $ n $. Encuentra todos los números $ n $ tales que $n = d_2 ^ 2 + d_3^3$.
Examenes de la Olimpiada Mexicana de Matemáticas por fin en MaTeTaM
Como seguramente ya lo habrán notado. Hemos estado agregando todos los problemas de todos los exámenes de la OMM.
Ojalá se tomen el tiempo de resolverlos todos y nos compartan sus soluciones.
A continuación escribo las ligas a cada uno de los exámenes de la Olimpiada Mexicana de Matemáticas, desde 1987 a 2009 2010:

P6 OMM 2006. Problema con números surtidos
Sea $n$ la suma de los dígitos de un entero positivo $A$. Decimos que $A$ es “surtido” si cada uno de los enteros $1,2,\ldots,n$ es suma de dígitos de $A$
- Demuestra que si $1,2,\ldots,8$ son sumas de dígitos de un entero $A$ entonces $A$ es surtido.
- Si $1,2,\ldots,7$ son sumas de dígitos de un entero $A$, ¿es $A$ necesariamente surtido?
Nota: El número 117 no es surtido pues sólo $1=1, 2 = 1+1, 7 = 7, 8 = 1 + 7, 9 = 1 + 1 + 7$ se pueden escribir como suma de dígitos de 117.
P5 OMM 2006. Altura de triángulo pedal
Sean $ABC$ un triángulo acutángulo y, $AD, BE$ y $CF$ sus alturas. La circunferencia con diámetro $AD$ corta a los lados $AB$ y $AC$ en $M$ y $N$, respectivamente. Sean $P$ y $Q$ los puntos de intersección de $AD$ con $EF$ y $MN$, respectivamente. Demuestra que $Q$ es el punto medio de $PD$.
