Publicaciones Recientes
Invitación a curso de matemáticas de concurso
Para iniciar a calentar el ambiente de las matemáticas de concurso en este año 2013, la UAMCEH-UAT y la Delegación Tamaulipas de la OMM invitan a todos los adolescentes menores de 15 de Tamaulipas a inscribirse en un
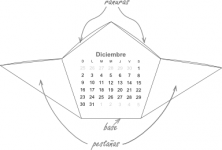
Calendario dodecaédrico con origami 2013
Para hacer el calendario sólo tienen que descargar, imprimir, doblar y armar. Aquí está el video con las intrucciones de armado que hicimos para la versión 2010.
Algunos de ustedes nos han comentado que les sobran muchas pestañas a la hora de armarlo. Les queremos decir que sí es posible armarlo sin pegamento y sin que sobren pestañas.
Efectos perversos de lo políticamente correcto
En el mes de noviembre pasado en México se le armó un escandalito al diputado Arellano por tratar de adornar su discurso con un refrán popular: "la tierra es como las mujeres, hay que trabajarla y abonarla" (http://www.proceso.com.mx/?p=324460).
Algunas diputadas consideraron ofensivo que se viera a la mujer como productora de niños y Arellano tuvo que disculparse y solicitar que se borrara esa frase de la minuta.

El fácil del concurso nacional de la XXVI OMM

XXVI OMM --los problemas del segundo día
Problema 4. A cada entero positivo se le aplica el siguiente proceso: al número se le resta la suma de sus dígitos, y el resultado se divide entre 9. Por ejemplo, el resultado del proceso aplicado al 938 es 102, ya que (938-(9+3+8))/9=102. Aplicando dos veces el proceso a 938 se llega a 11, aplicado 3 veces se llega al 1. Cuando a un entero positivo $n$ se le aplica el proceso una o varias veces, se termina en 0. Al número al que se llega antes de llegar al 0, lo llamamos la casa de $n$. ¿Cuántos números menores que 26000 tienen la misma casa que 2012?
XXVI OMM --los problemas del primer día
Problema 1. Sean $C_1$ una circunferencia con centro $O$, $P$ un punto sobre ella y $l$ la recta tangente a $C_1$ en $P$. Considera un punto $Q$ sobre $l$, distinto de $P$, y sea $C_2$ la circunferencia que pasa por $O, P$ y $Q$. El segmento $OQ$ intersecta a $C_1$ en $S$ y la recta $PS$ intersecta a $C_2$ en un punto $R$ distinto de $P$. Si $r_1$ y $r_2$ son las longitudes de los radios de $C_1$ y $C_2$, respectivamente. Muestra que $PS/SR=r_1/r_2$.
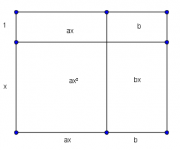
Razonamiento diagramático --en problemas de factorización
En este post voy a comentar sobre el método de reagrupamiento para factorizar una ecuación cuadrática y su correspondiente solución diagramática. Ilustro con un caso particular de toda
Una familia de problemas cuadráticos
En una ecuación cuadrática, si se puede factorizar entonces se puede representar como rectángulo --con uno de sus factores la base y el otro la altura.
Consideremos el problema de factorizar la ecuación cuadrática
$$ax^2+(a+b)x+b=0$$
(donde $a,b$ son enteros positivos).
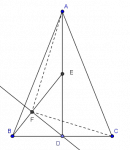
Un problema geométrico --propuesto por Orlando Ochoa
En el entrenamiento de la semana pasada (19, 20 y 21 de octubre) le tocó a Orlando Ochoa Castillo decidir la selección Tamaulipas de la XXVI OMM --con su entrenamiento y su examen selectivo del domingo en la mañana.
El viernes 19 me tocó recibir a Orlando (a las 4 PM) y presentarlo a los preseleccionados. Orlando inició su entrenamiento con el problema que abajo se dicute. Yo decidí quedarme un rato en el aula en que tuvo lugar la sesión de Orlando y, sin más que hacer, me puse a resolverlo... (pero al final tuve que recurrir a la geometría analítica pues la idea creativa no llegó a mi cabeza...). El problema es el siguiente:
Selección Tamaulipas para la XXVI OMM
Un poco tarde pero aquí está la selección que acudirá al concurso nacional de la Olimpiada Mexicana de Matemáticas el próximo mes de noviembre.
Claudia Lorena Cabrera Arjona
Oscar Gilberto Brewer De la Vega
Eduardo Alexis Romo Almazán
Emmanuel Sanchez Sandoval
Gerardo Cantú González
Mariano Narváez Pozos
Sacnicté
De vez en cuando se encuentra uno con verdaderos talentos adolescentes dentro del campo de las matemáticas escolares.
Se puede decir que todos los adolescentes son iguales (tienen las mismas capacidades intelectuales). Sólo que "algunos son más iguales que otros" (para usar la famosa frase de George Orwell en la novela satírica denominada Rebelión en la Granja --Animal Farm).
Sacnicté: veni, vidi, vici
Sacnicté, la niña del COBAT 06 (de Ocampo), quien resolvió correctamente tres de los 4 problemas del concurso estatal de la OMM Tamaulipas 2012, es igual que todos los 102 participantes en ese concurso... sólo que es un poquito más igual que ellos.
