En este post voy a continuar el post anterior sobre vectores añadiendo dos operaciones adicionales a las ya abordadas (suma y resta y multiplicación por un escalar).
Se trata del producto interior (o escalar o punto) entre dos vectores y el producto área (o exterior o cruz), los cuales aportan, respectivamente, sendos criterios para la perpendicularidad y la colinealidad de vectores. Se discuten algunas instancias de uso para demostrar el potencial de los vectores en el problem solving de geometría. Voy a iniciar con un
Problema elemental de geometría analítica
Los vértices $A$ y $B$ de un triángulo tienen coordenadas $A=(0,0), B=(3,1)$. Calcular las coordenadas del vértice $C$ si se sabe que está en el primer cuadrante y en la recta $x-2y+2=0$, y que el área del triángulo es 2.
Solución
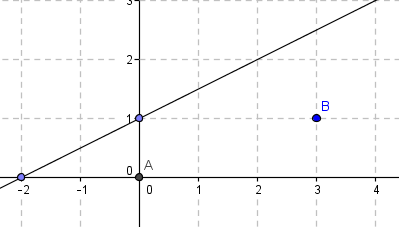
Un análisis preliminar revela que el vértice $C$ debe estar en una paralela a la recta que pasa por $A$ y $B$ a una distancia de $4/\sqrt{10}$ (pues la base $AB$ mide $\sqrt{10}$). Pero también está en la recta $x-2y+2=0$ --por dato. Así que la respuesta será el punto de intersección de las dos rectas.
Puesto que la recta por $A$ y $B$ tiene como ecuación $y=x/3$, entonces su pendiente es 1/3. Así que la recta paralela a $AB$ tiene como ecuación $y=x/3+b$. Ahora el problema se reduce a encontrar $b$ --su ordenada al origen.
Sean $P=(0,b)$ el punto en que $y=x/3+b$ corta al eje $y$, $Q=(-3b,0)$ el punto en que corta al eje $x$, $O=(0,0)$ el origen, y $S$ el pie de la perpendicular a $AB$ bajada desde $P$.
Entonces los ángulos $OQP$ y $OPS$ son iguales --por tener lados mutuamente perpendiculares. En consecuencia, los triángulos $PQO$ y $OPS$ son semejantes --por AAA. Esto permite calcular $b=4/3$ --calculando primero $PQ$ (mediante las proporciones adecuadas) y después $b$ (por Pitágoras en el triángulo $PQO$). Así que el plan se consuma encontrando la intersección de las dos rectas mencionadas. Esa intersección es $C=(2,2) y es la respuesta al problema.
Comentario
En su aparente simplicidad, el problema es difícil. Su dificultad principal radica en el cálculo de la ordenada al origen $b$. Pues ahí se tuvo que recurrir a la geometría sintética --la semejanza de dos triángulos y Pitágoras.
Pero se suponía que la geometría analítica debería convertir el problema a puro cálculo algebraico --y es precisamente esta perspectiva la que hace difícil la resolución.
Por otro lado, si uno supiera todos los trucos de la geometría analítica, la solución sí llega a simplificarse. Algunos de estos trucos los veremos después de definir otras
Dos operaciones con vectores
Aparte de la operación de multiplicación de un vector por un escalar (un número real), la cual quedó implícita en el post anterior, vamos a definir aquí el producto interior y el producto "perp" (o producto área) de dos vectores.
El producto interior de los vectores de posición $\vec{A}=(x_A,y_A)$ y $\vec{B}=(x_B,y_B)$ se define como $\vec{A}\cdot\vec{B}=(x_Ax_B,y_Ay_B)$.
Como una consecuencia inmediata se tiene que el producto interior de un vector $\vec{A}=(x_A,y_A)$ por sí mismo es el cuadrado de su longitud (o norma o módulo): $\vec{A}\cdot\vec{A}=x_A^2+y_A^2$.
Es inmediato también que cumple la propiedad conmutativa: $\vec{A}\cdot\vec{B}=\vec{B}\cdot\vec{A}$.
Y no tan inmediato es el hecho de que el producto interior cumple la ley distributiva:
$$\vec{A}\cdot(\vec{B}+\vec{C})=\vec{A}\cdot(x_B+x_C,y_B+y_C)$$
$$=(x_A(x_B+x_C),y_A(y_B+y_C))=(x_Ax_B+x_Ax_C,y_Ay_B+y_Ay_C))$$
$$=(x_Ax_B,y_Ay_B)+(x_Ax_C,y_Ay_C)=\vec{A}\cdot\vec{B}+\vec{A}\cdot\vec{C}$$
Otra definición del producto interior de dos vectores
Veamos ahora que es posible dar otra definición más geométrica del producto interior de dos vectores $\vec{A}$ y $\vec{B}$. Pero antes hay que darse cuenta que los vectores de posición $\vec{A}$ y $\vec{B}$ forman un triángulo con el vector $\vec{B}-\vec{A}$. (Y entonces se puede aplicar la ley de los cosenos al triángulo formado por sus módulos.)
$$|\vec{B}-\vec{A}|^2=(\vec{B}-\vec{A})\cdot(\vec{B}-\vec{A})$$
$$=(\vec{B}-\vec{A})\cdot\vec{B}-(\vec{B}-\vec{A})\cdot\vec{A})$$
$$=\vec{B}\cdot\vec{B}-\vec{A}\cdot\vec{B}-\vec{B}\cdot\vec{A}+\vec{A}\cdot\vec{A}$$
$$=|\vec{A}|^2+|\vec{B}|^2-2\vec{A}\cdot\vec{B}$$
En resumen,
$$|\vec{B}-\vec{A}|^2=|\vec{A}|^2+|\vec{B}|^2-2\vec{A}\cdot\vec{B}$$
Pero $$\vec{A},\vec{B},\vec{B}-\vec{A}$$
forman un triángulo (a menos que $\vec{A},\vec{B}$ sean colineales) y sus módulos son precisamente las longitudes.
Comparando con la ley de cosenos ($c^2=a^2+b^2-2abcos\theta$) y restando se establece la ecuación
$$\vec{A}\cdot\vec{B}=|\vec{A}||\vec{B}|cos\theta$$
Y ésta es la otra definición del producto punto de dos vectores.
Una definición equivalente muy importante. Porque, viéndola geométricamente, $|\vec{B}|cos\theta$ es la proyección ortogonal del vector $\vec{B}$ sobre el vector $\vec{A}$.
El producto-área
Ahora bien, con ésta interpretación, el vector $\vec{A}$ girado sobre el origen 90 grados multiplicado interiormente (en el sentido de producto interior) por el vector $\vec{B}$, da como resultado el área del paraleogramo formado por los vectores $\vec{A}$ y $\vec{B}$ --pues los módulos del vector $\vec{A}$ y éste mismo pero girado 90 grados son iguales, y la proyección del $\vec{B}$ sobre el A girado es la altura del paralelogramo.
Otras soluciones al problema planteado al principio
Solución alternativa 1 (por vectores)
Si uno supiera que el vector $\vec{AB}$ (o sea $B=(3,1)$) girado 90 grados es $P=(-1,3)$, y si recordara que el producto interior de éste con el $\vec{OC}$ (el buscado) es el área del paralelogramo formado por ellos, entonces la solución sale en dos patadas. Porque ello permite formar la ecuación
$$4=\vec{OP}\cdot\vec{OC}=(-1,3)\cdot(2y-2,y)$$
Y la solución se hace evidente: $C=(2,2)$.
(Claramente, el otro $C$ que cumple se obtiene tomando como $P$ el simétrico del ya usado, es decir, $P=(1,-3)$. Con lo cual se obtiene $C=(-14,-6)$.)
Solución alternativa 2 (usando la fórmula del área como determinante)
Si bajamos perpendiculares desde los vértices al eje x se puede obtener el área del triángulo --si se conocieran las coordenadas de los puntos. Como $A$ es el origen, $B=(3,1)$ y $C=(2y-2,y)$, entonces obtenemos el área del triángulo (que es 2) sumando las áreas del triángulo formado por el origen, el punto C y el eje x más el trapecio formado por los puntos B y C y el eje x, y finalmente restamos el área del triángulo formado por A, B y el eje x.
$$4=2(ABC)=(2y-2)y+(y+1)(3-2y+2)-3(1)=y+2$$
De aquí que $y=2,x=2$.
De paso, hay que decir que éste el procedimiento para obtener la fórmula del determinante para obtener el área de un triángulo.
Otros problemas de geometría resueltos con vectores
El triàngulo $ABC$ es isósceles, con $AB=AC$ y circuncentro $O$. Sean $D$ el punto medio de $AB$ y $E$ el baricentro de $ACD$. Demostrar que $OE$ es perpendicular a $CD$.
Soluciòn (con vectores)
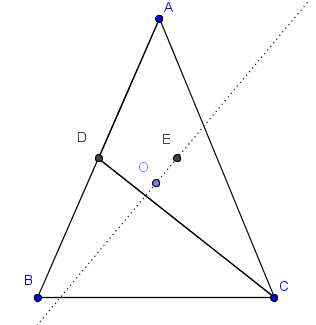
Sea $O$ el origen de coordenadas y designemos con $\vec{a},\vec{b},\vec{c},\vec{d},\vec{e}$ a los vectores de posición correspondientes a los puntos $A,B,C,D,E$, respectivamente. Vamos a demostrar que $\vec{e}\cdot\vec{CD}=0$.
Como se sabe (teorema conocido)
$$\vec{e}=\frac{\vec{a}+\vec{b}+\vec{c}}{3}$$
$$\vec{d}=\frac{\vec{a}+\vec{b}}{2}$$
Por otro lado, $\vec{CD}=\vec{d}-\vec{c}$. Veamos ahora si el producto interno se anula:
$$\vec{e}\cdot(\vec{d}-\vec{c})=\frac{\vec{a}+\vec{c}+\frac{\vec{a}+\vec{b}}{2}}{3}\cdot\frac{\vec{a}+\vec{b}-2\vec{c}}{2}$$
$$=\frac{(2\vec{a}+2\vec{c}+\vec{a}+\vec{b})^2}{12}$$
$$12\vec{e}\cdot(\vec{d}-\vec{c})=3\vec{a}\cdot\vec{a}+3\vec{a}\cdot\vec{b}-6\vec{a}\cdot\vec{c}$$
$$+\vec{b}\cdot\vec{a}+\vec{b}\cdot\vec{b}-2\vec{b}\cdot\vec{c}+2\vec{c}\cdot\vec{a}$$
$$+2\vec{b}\cdot\vec{c}-4\vec{c}\cdot\vec{c}$$
$$=3|\vec{a}|^2+|\vec{b}|^2-4|\vec{c}|^2+4\vec{a}\cdot\vec{b}-4\vec{a}\cdot\vec{c}$$
$$=4\vec{a}\cdot(\vec{b}-\vec{c}=0$$
Pues en isósceles, la mediatriz es mediana.