Blog de jmd
¿Dijiste recursión?
Notación sumatoria e instancias de uso
Quizá una de las razones por las que no se enseña la notación sumatoria en la escuela, y se espera hasta el cálculo o hasta la estadística descriptiva en el bachillerato o la universidad, es porque antes no se necesita. Es muy útil cuando se necesita saber si una serie infinita converge --y el tema de las series infinitas es del cálculo. Pero se puede abordar antes del cálculo, en el tema de sucesiones aritmética y geométrica y sucesiones recursivas, a lo cual puede seguir el de ciertos trucos para resolver ecuaciones de recurrencia elementales como la transformada Z.
Calidad educativa y bienes sustitutos
Como se sabe, si no hay para la mantequilla la margarina está bien. La margarina sustituye en casi todo a la mantequilla, sólo que no es mantequilla ("al que quiere azul celeste...). Es un hecho de la vida que la calidad es inaccesible para la mayoría. Pero no hay problema, porque siempre habrá un producto que sustituye al de calidad (en casi todo). Es decir, casi siempre se encuentra un bien sustituto que tiene casi la misma utilidad que el inaccesible.
Obstáculo epistemológico
Ahora que está de moda hablar del constructivismo como método de enseñanza (gracias a las últimas reformas en educación, para bien o para mal), es posible que sea de alguna utilidad para los lectores adultos de MaTeTaM, dedicar unos minutos a elaborar un poco sobre sus conceptos un tanto esotéricos --situación didáctica, con
El diagrama: ¿facilita realmente el razonamiento?
La respuesta a la pregunta del título es: depende del razonador. Esta respuesta la derivé de una experiencia de enseñanza que a continuación narro y comento.
En estos días, dentro del tema de geometría, traté de enseñarles a dos jóvenes universitarios el teorema de Pitágoras. Es decir, la demostración de ese famoso teorema. Fue de hecho un experimento didáctico, solamente para comprobar que a un estudiante profesional (es decir, que el ser estudiante ha sido su modus vivendi por al menos 13 años) le resulta casi imposible concentrarse en una tarea de este tipo.

Competencias comunicativas y cognitivas en la RIEMS
Como se sabe (o se debería saber) el razonamiento está ligado al lenguaje, en particular a la competencia lingüística del hablante. La hipótesis dominante en esta área de la investigación científica es la de Vygotsky: lenguaje y pensamiento son interdependientes (es decir, se determinan mutuamente). (Esta hipótesis ha dado origen a la psicolingüística.) Otras posiciones (hipótesis) son posibles y todas han sido posiblemente defendidas por los estudiosos de la filosofía y la lingüística.
Pensar matemáticamente
Ahora que está de moda hablar (en educación matemática) de matematizar, situaciones reales o formales, como una vía para enseñar matemáticas en la escuela, puede ser de alguna utilidad tematizar este verbo en un post de MaTeTaM. Ver mi post sobre Letracidad Matemática
Otra forma de ver Cauchy
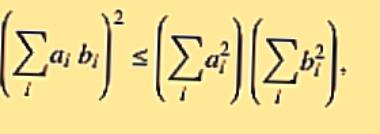
Si no se puede expresar, lo mejor es callar
¿Alguien se ha dado cuenta de que es necesario censurar y editar nuestro lenguaje? Quiero decir, ante el riesgo de interpretaciones equivocadas en términos de ecología, de género, de protección a los animales, etc. Por ejemplo, tomemos el caso de los modos femeninos de interpretar y procesar la información.
