Julio 2009
La complejidad de un problema geométrico: a propósito del 8(G) del concurso estatal
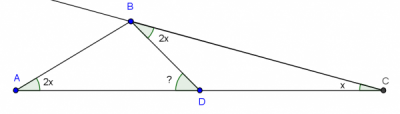
Reto para novicios: el problema 4 de la IMO 2009 (invertido y con 4 incisos)
Aprovechando el entusiasmo de Brandon voy a poner aquí una variante del problema 4 de la IMO 2009, desglosándolo e invirtiéndolo con la idea de reducir su complejidad. Pero antes de plantear el reto a los miembros de la preselección Tamaulipas 2009, permítaseme comentar dos o tres cosas sobre ese problema, sobre su dificultad.
El poder cognitivo de un framing
Argumentos básicos de conteo
Con este post estoy inaugurando una sucesión que podría llegar hasta 20. La idea es la misma que la que usé con los GBC-teoremas, es decir, formular una serie de hechos básicos sobre el tema. En los teoremas de geometría básica del círculo me vi limitado por el formato de teorema y no añadí comentarios u otras ayudas didácticas. Es por eso que ahora, para los hechos básicos de combinatoria, elijo la entrada de blog para difundir es conocimiento básico, dada la flexibilidad de su formato.
Argumentos básicos de conteo 2 (r-listas)
Argumentos básicos de conteo 3 (Combinaciones)
Intro
En este post vamos a derivar la fórmula para las combinaciones de n objetos tomados de r en r. Así se decía antes, ahora se prefiere decir el número de subconjuntos de tamaño r tomados de un conjunto de tamaño n. De nuevo, aquí lo importante es el razonamiento combinatorio que da lugar a la fórmula.
