Intermedio

Encontrar todos los números primos $p,q$ tales que $p$ divide a $q+6$ y $q$ divide a $p+7$.

Se marcan los puntos A, B, C, D sobre una recta, en ese orden, con AB y CD mayores que BC. Se construyen triángulos equiláteros APB, BCQ y CDR, con P, Q y R del mismo lado respecto a AD. Si el ángulo PQR mide 120 grados, pruebe que

Un entero positivo se denomina tico si es el producto de tres números primos diferentes que suman 74. Verifique que 2014 es tico. ¿Cuál será el próximo año tico? ¿Cuál será el último año tico de la historia?

3.N. Encontrar todos los números primos que pueden escribirse como la diferenciade dos primos y como la suma de dos primos. (Nota: el 1 no es primo.)

2.6. Considere las ecuaciones cuadráticas

2.5. Sea ABC un triángulo acutángulo isósceles con AC=BC. M y N son los puntos medios de AC y BC, respectivamente. La altura desde A corta a la prolongación de MN en X y la altura desde B corta a la prolongación de MN en Y. Z es la intersección de AY con BX. Además, sucede que los triángulos ABC y XYZ son semejantes. Determina la razón $\frac{AC}{AB}$.

2.4. Se tiene una tabla con siete columnas A,B,C,D,E,F,G y se coloca en ella los números naturales que no contienen al 3 o al 7 en su desarrollo decimal. Se empieza en la casilla C1, como se muestra. ¿En cuál columna y renglón queda el 2014?

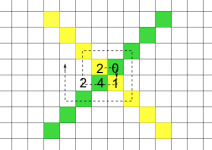
2.3. Sobre una cuadrícula se coloca 2014 veces el número 2014 (un dígito en cada casilla) siguiendo una espiral como se muestra en la figura. Sea M la suma de los números sobre las casillas verdes y N la suma de los números sobre las casillas amarillas. Calcula la diferencia entre M y N.

1.6. Sean ABC un triángulo acutángulo, H su ortocentro y M el punto medio de BC. La perpendicular a MH por H corta a AB en L y a AC en N. Demuestra que LH=HN.