Publicaciones Recientes
XXIV Olimpiada Iberoamericana de Matemáticas (problema 4)
Sea ABC un triángulo con AB≠AC. Sean I el incentro de ABC y P el otro punto de intersección de la bisectriz exterior del ángulo A con el circuncírculo de ABC. La recta PI intersecta por segunda vez al circuncírculo de ABC en el punto J. Demostrar que los circuncírculos de los triángulos JIB y JIC son tangentes a IC y a IB, respectivamente.
Olimpiada Iberoamericana de Matemáticas 2009
Hoy inició la XXIV Olimpiada Iberoamericana de Matemáticas en la Ciudad de Querétaro, México. Es decir, hoy los adolescentes aspirantes a una medalla presentaron la primera parte del examen, consistente en tres problemas. Mañana presentan los siguientes tres, con lo cual la suerte estará echada...

XXIV Olimpiada Iberoamericana de Matemáticas (problema 3)
Sean C1 y C2 dos circunferencias de centros O1 y O2, con el mismo radio, que se cortan en A y en B. Sea P un punto sobre el arco AB de C2 que está dentro de C1. La recta AP corta a C1 en C, la recta CB corta a C2 en D y la bisectriz del ∠CAD intersecta a C1 en E y a C2 en L. Sea F el punto simétrico a D con respecto al punto medio de PE. Demostrar que existe un punto X que satisface ∠XFL=∠XDC=30∘ y CX=O1O2.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 2)
Para cada entero positivo n se define an=n+m, donde m es el mayor entero tal que 22m≤n2n. Determinar qué enteros positivos no aparecen en la sucesión an.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 1)
Sea n un natural mayor que 2. Supongamos que n islas están ubicadas en un círculo y que entre cada dos islas vecinas hay dos puentes como en la figura:
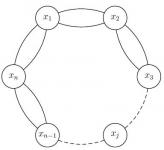
Olimpiada Mexicana de Matemáticas (Del. Tam. 2009): Recordatorio de entrenamiento
Les recuerdo a los 16 preseleccionados que el entrenamiento pre-norestense se llevará a cabo los días 26 y 27 (sábado y domingo) en las instalaciones de la UAMCEH-UAT.
Olimpiada Iberoamericana (el 4 de 2008)
Demuestra que no existen enteros positivos x,y tales que x2008+2008!=21y
Olimpiada Iberoamericana (el 4 de 2004)
Determinar todas las parejas (a,b), donde a,b son enteros positivos de dos dígitos cada uno, tales que 100a+b y 201a+b son cuadrados perfectos de cuatro dígitos.
Olimpiada Iberoamericana (el 5 de 1985)
A cada número natural n se le asigna un entero no negativo f(n) de tal manera que se satisfacen las siguientes condiciones:
- (i) f(rs)=f(r)+f(s)
- (ii) f(n)=0, si el dígito de las unidades de n es 3
- (iii) f(10)=0
Hallar f(1985)
Olimpiada Iberoamericana (el 1 de 1999)
Halla todos los enteros positivos que son menores que 1000 y cumplen con la siguiente condición: el cubo de la suma de sus dígitos es igual al cuadrado de dicho entero.
