Publicaciones Recientes
Reducción de números
Un entero positivo $a$ se reduce a un entero positivo $b$, si al dividir $a$ entre su dígito de las unidades se obtiene $b$. Por ejemplo, 2015 se reduce a $\frac{2015}{5}=403$. Encuentra todos los enteros positivos que, mediante algunas reducciones, llegan al número 1. Por ejemplo, el número 12 es uno de tales enteros pues 12 se reduce a 6 y 6 se reduce a 1.
Coloración en números del 1 al 4027
Cada uno de los números del 1 al 4027 se ha coloreado de verde o de rojo. Cambiar el color de un número es pasarlo a verde si era rojo, y pasarlo a rojo si era verde.
Diremos que dos enteros positivos $m$ y $n$ son cuates si alguno de los números $\frac{m}{n}$ o $\frac{n}{m}$ es un número primo. Un paso consiste en elegir dos números que sean cuates y cambiar el color de cada uno de los números.
Muestra que después de realizar algunos pasos es posible hacer que todos los números del 1 al 2014 sean verdes.
Sobre el problema 3 del selectivo final
El problema y la solución de Germán
Selección Tamaulipas OMM_2014
La suerte fue echada el domingo 12 con el selectivo final y los dados muestran hoy los resultados. Tenemos selección y MaTeTaM felicita a sus integrantes:
Germán Puga Castillo
Roberto Alain Rivera Bravo
José Luis Domínguez Rodríguez
Julio Cesar Sandoval de la Cruz
Roberto Llanos Hernández
Jesús Francisco Anaya González
Vaya una felicitación muy especial para Jesús, un joven con mucho futuro en la olimpiada (podrá ir en 2015 y 2016) --bueno si, como me gustaría esperar, no se estaciona en los bronces....
Los saluda
jmd
Selectivo final (OMM_Tam_2014)
1. Los números del 1 al 28 se acomodan al azar en una cuadrícula de $4\times7$ (4 filas y 7 columnas, un número en cada cuadrito). A continuación se consideran los productos $P_1$ de todos los números en la primera fila, $P_2$ el de todos los números en la segunda fila y, de la misma manera, se obtienen $P_3$ y $P_4$. Demuestra que alguno de estos cuatro productos es múltiplo de 128.
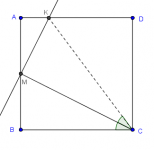
2. Sea K un punto sobre el arco AB del circuncírculo del triángulo isósceles $ABC$ (con AB=BC). Demuestra que $$AK\cdot{KC}=AB^2-KC^2$$
Así queda la preselección después del selectivo 4
|
|
Nombre |
S4 |
S3 |
total |
|
|
Germán Puga Castillo |
21 |
Focos distribuidos en una circunferencia (P1)
Se tienen 25 focos distribuidos de la siguiente manera: los primeros 24 se disponen en una circunferencia colocando un foco en cada uno de los vértices de un 24-ágono regular, y el foco restante se coloca en el centro de dicha circunferencia. Se permite aplicar cualquiera de las siguientes dos operaciones:
Cuadrilátero cíclico: más instancias de uso
En este post voy a recomendar el estudio de algunos materiales sobre cuadriláteros cíclicos a quienes se están preparando para el nacional. De paso intercalo dos instancias de su uso.
En un post anterior --dedicado a los criterios de reconocimiento de los cuadriláteros cíclicos-- hemos destacado la importancia de esta herramienta en el problem solving de geometría y discutimos varias instancias de uso asociadas a demostraciones del teorema de la mariposa.
Modelación de problemas. Cálculo diferencial e integral I.
1. Se desea cercar un terreno de 2000m2, expresa una ecuación que defina la cantidad de cerco en función de su lado de mayor longitud. Nota: Es un terreno rectangular.
2. Expresa el área de una caja con base cuadrangular si tiene un volumen de 16m2 expresala en función de la longitud de su altura.
3.Se desea construir un cilindro de 40 cm3, expresa el área del cilindro en función de su radio.
