Publicaciones Recientes
L1.P9 (Dimes y quarters)
Ana fue a McAllen el fin de semana con sus papás. Éstos le regalaron dimes (10 centavos) y quarters (25 centavos). Si los dimes fuesen quarters y los quarters fueran dimes Ana tendría un dollar y 5 centavos (de dollar) menos de lo que ahora tiene.
L1.P8 (Generalización del L1.P7)
Demostrar que si $ k,n$ son enteros positivos sin divisores en común ($k,n$ primos relativos), entonces el máximo entero positivo que no se puede expresar como suma de múltiplos de $k$ y $n$ es $kn-k-n.$
L1.P7 (No expresable como n=4x+5y)
Encontrar el máximo entero positivo $ n $ que no se puede expresar en la forma $n=4x+5y$, con $x,y$ enteros positivos.
L1.P6 (Problema cuadrático)
Si $p^2+1/p^2=7$, con $p$ entero positivo, encontrar el valor de $p+1/p.$
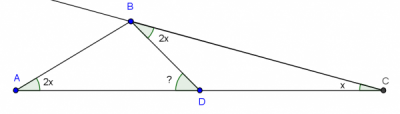
L1.P5 (Encontrar ángulo con isósceles)
En un triángulo $ ABC $ los lados $ AC $ y $ BC $ son iguales. Un punto $D$ en el lado $ BC $ es tal que los triángulos $ABD$ y $ACD$ son isósceles. Si $AD=AB$ ¿cuánto mide el ángulo en $B$?
L1.P4 (Fracciones a/b menores que 1)
Si $a, b$ son dígitos (elementos del conjunto $\{1,2,3,4,5,6,7,8,9\}$), encontrar el número de fracciones $a/b$ menores que 1.
L1.P3 (Menor entero que no divide a 69!)
Para un entero positivo $ n $, el factorial de $ n $ (denotado con $n!$) es $n!=(n)(n-1)(n-2)...(3)(2)(1)$. Encontrar el menor entero positivo (distinto de 1) que no divide a 69!
L1.P2 (Lado de un cuadrado)
En un círculo de centro $O$ y radio $5k$, se traza un cuadrado. Uno de sus lados es cuerda de la circunferencia y el lado opuesto a la cuerda pasa por el centro $O$. Calcular la longitud del lado del cuadrado en términos de $k$.
Lista1.Problema1 (Residuo de 155/n)
El residuo que deja 80 al dividir entre un número entero positivo $ n $ es 4 ¿Cuál es residuo que deja 155 al dividirlo entre $ n $?
La complejidad de un problema geométrico: a propósito del 8(G) del concurso estatal