Publicaciones Recientes
Concurso ciudades de la XXIII OMM, el 27 de marzo
Enseguida se muestran las ciudades y sedes para el concurso ciudades (etapa municipal) de la Olimpiada Mexicana de Matemáticas en Tamaulipas.
El "maistro" más marrulla del ejido
Abel, Bocho y Casiano, tres "maistros" especialistas en construcción de bardas de adobón, ganaron un contrato para construir una.
Un chico fresa
Blaine, un chico fresa de la ciudad, se fue a "macalear" (de compras a McAllen) el fin de semana. Se compró una cachucha, una playera y un par de zapatos tenis.
Alturas de un isósceles
En un triángulo acutángulo $ ABC $, las alturas de $ B $ y $ C $ respecto a las bases $ CA $ y $ AB $, respectivamente, se intersectan en el punto $ S $. Sean $ M $ en $ AB $ y $ N $ en $ CA $ los pies de esas alturas. Demostrar que $AB=CA$ si y sólo si el ángulo $ MSB $ mide el doble que el ángulo $ CBN $.
Juego de las 3 cartas
Tres jugadores, $A, B, C$, utilizan tres cartas para jugar. Es cada una de ellas está escrito un número entero positivo y todos son diferentes, digamos $p, q, r$ en orden creciente.
Factores de 39
Si $m, n$ son enteros positivos que cumplen la ecuación $m^n+m^{n+1}+m^{n+2}=39$ encuentra sus valores (todos los posibles).
El profesor informado --y el tutor inteligente
Conocer la cultura matemática –el tránsito de novicio a experto.
Introducción
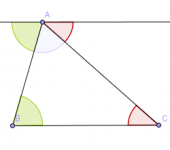
Uno de los teoremas más básicos de la geometría euclideana es el de la suma de ángulos internos de un triángulo (de hecho, por ser tan elemental, no es claro que se le pueda llamar teorema). Para el principiante que ve su demostración diagramática por primera vez, la interpretación del diagrama puede llegar a ser una experiencia visual muy gratificante: trazas una paralela a un lado por el vértice opuesto a ese lado y el resultado se hace evidente.
Tendencias de la educación matemática (a través de un problema razonado)
La siguiente reflexión está inspirada en algún post que vi en algún lugar de internet en el año 2004 (visiten mi blog que tengo abandonado en blogspot: http://mat
Teorema de Napoleón (interior)
Si en un triángulo $ ABC $ se construyen triángulos equiláteros interiores sobre sus lados, entonces los centros $X, Y, Z$ de dichos triángulos equiláteros determinan un triángulo equilátero $ XYZ $, conocido como triángulo de Napoleón interior. (Demostrarlo.)
