Publicaciones Recientes
Selectivo 2 OMM_Tam_2014
Enseguida presento los cuatro problemas del segundo examen selectivo para la preselección Tamaulipas OMM 2014. Añado las soluciones al 2 y al 4.
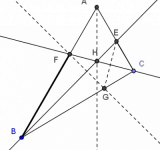
Problema 1. En un cuadrilátero ABCD convexo se trazan las perpendiculares desde cada vértice a la diagonal que no pasa por él. Demostrar que los cuatro puntos de intersección de cada perpendicular con su correspondiente diagonal forman un cuadrilátero semejante al dado.
Preselección OMM Tamaulipas 2014 --después del primer corte
1 Germán Puga Castillo
2 Roberto Alain Rivera Bravo
3 José Luis Domínguez Rodríguez
4 Roberto Llanos Hernández
5 Pablo Aurelio Estrada Flores
6 Jesús Francisco Anaya González
7 Julio Cesar Sandoval de la Cruz
8 Ingrid Amaya Chávez
9 Carlos Humberto Luévanos Méndez
10 Marlene Sandoval M
11 Mario Arturo González Sandoval
12 Juventino López Jerónimo
13 Sergio Gutiérrez González
14 Javier Alfonso Martiarena Hernández
15 Alan Alfredo Reta Ramírez
Relaciones combinatorias
Sean $r,n$ enteros no negativos tales que $r\leq{n}$.
a) Demostrar que $$\frac{n+1-2r}{n+1-r}C(n,r)$$ es un entero.
b) Demostrar que
$$ \sum_{r=0}^{\lfloor n/2\rfloor}\frac{n+1-2r}{n+1-r}C(n.r)<2^{n-2}$$ para todo $n\geq 9$.
(Nota: $\lfloor x\rfloor$ es el mayor entero menor o igual que x, y $C(n,r)$ es el número de subconjuntos de tamaño r tomados de un conjunto de tamaño n.)
Viaje redondo
Air Michael y Air Patrick operan vuelos directos que conectan Belfast, Cork, Dublin, Galway, Limerick y Waterford. Para cada par de ciudades exactamente una de las aerolíneas opera la ruta (en ambos sentidos) conectando las ciudades.Demostrar que hay cuatro ciudades para las cuales una de las aerolíneas opera un viaje redondo. (Un viaje redondo para las ciudades P,Q,R,S es un viaje que va de P a Q, de Q a R, de R a S y de S a P.)
Senos cuadráticos
Todos los primos tales que...
Encontrar todos los números primos $p,q$ tales que $p$ divide a $q+6$ y $q$ divide a $p+7$.
Una recta variable que pasa por un punto fijo
El punto P está fijo en una circunferencia y el punto Q está fijo en una recta. Un punto variable R se mueve sobre la circunferencia pero sin alinearse con P y Q. La circunferencia por P,Q y R corta a la recta de nuevo en V. Demostrar que la recta VR pasa por un punto fijo.
Resultados del primer selectivo OMM_Tam_2014
A continuación se presentan los resultados del primer selectivo OMM Tamaulipas 2014. ¡Ánimoooo!
Primos y divisibilidad: dos problemas
Voy a comentar en este post las soluciones de los problemas 1 y 2 del primer selectivo para la preselección OMM Tamaulipas 2014. Espero que sirva como feedback para los preseleccionados que no los resolvieron o los resolvieron de otra forma. (Vaya una felicitación para Camilo por su excelente elección de los problemas.)
Problema 1. Sean m,n enteros positivos tales que $m^2+n^2$ es múltiplo de 3. Pruebe que m y n son también múltiplos de 3.
Comentario:
Examen selectivo 1, OMM_Tam_2014
El fin de semana (8,9 y 10 de agosto) se llevó a cabo el primer entrenamiento de la preselección OMM Tamaulipas 2014 y se realizó el primer examen selectivo, el cual reproduzco a continuación.
El entrenamiento estuvo a cargo de Luis Camilo Castillo Toledano (las gracias le sean dadas) y el tema fue teoría de números.
Problema 1. Sean $m,n$ enteros positivos tales que $m^2+n^2$ es múltiplo de 3. Pruebe que $m$ y $n$ son también múltiplos de 3.
Problema 2. Encontrar todos los números primos $p,q$ tales que su suma y su diferencia también son números primos.
