Publicaciones Recientes
Triángulo escaleno (P2)
Sea $ABC$ un triángulo escaleno, $D$ el pie de la altura desde $A$, $E$ la intersección del lado $AC$ con la bisectriz del lado $\angle ABC$, y $F$ un punto sobre el lado $AB$. Sea $O$ el circuncentro del triángulo $ABC$ y sean $X$, $Y$ y $Z$ los puntos donde se cortan las rectas $AD$ con $BE$, $BE$ con $CF$, $CF$ con $AD$, respectivamente. Si $XYZ$ es un triángulo equilátero, demuestra que uno de los triángulos $OXY$, $OYZ$, $OZX$ es un triángulo equilátero.
Moscas en un cubo (P1)
En cada uno de los vértices de un cubo hay una mosca. Al sonar el silbato cada una de las moscas vuela a alguno de los vértices del cubo situado en una misma cara del vértice de donde partió, pero diagonalmente opuesto a éste. Al sonar el silbato ¿de cuántas maneras pueden volar las moscas de modo que en ningún vértice queden dos o más moscas?
Discusión sobre incírculos y excírculos
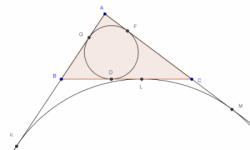
Voy a discutir en este post algunos conceptos relacionados con las circunferencias incrita y exinscrita. Dichos conceptos forman un todo y conviene aprenderlos en paquete --es muchísimo más fácil retenerlos en la memoria y comprenderlos si se aprenden en sus interconexiones.
Se trata de los conceptos de semiperímetro --en el contexto de ciertas simetrías entre las longitudes de las tangentes de circuncírculo y excírculos--, el concepto de puntos isotómicos, y el de los puntos de Gergonne y Nagel --como ejemplo de puntos conjugados isotómicos.
Concurso MaTeTaM
Debido a cuestiones fuera del control de la delegación Tamaulipas de la OMM (Olimpiada Mexicana de Matemáticas), el proceso de selección en Tamaulipas se ha retardado demasiado este año.
Por esa razón, MaTeTaM solicita la opinión de los estudiantes y profesores asesores de Tamaulipas acerca de su posible participación en un concurso vía Internet a través de este sitio Web.
De ese concurso se obtendría --con la validación del delegado-- una preselección de 20 alumnos y los entrenamientos y exámenes selectivos (para elegir los 15 de la Olimpiada Norestense) iniciarían una vez regresando de las vacaciones en la segunda quincena de agosto.
Un problema clásico de homotecia
Durante el año 2009, al final de uno de los entrenamientos de la OMM Delegación Tamaulipas, Jesús Rodríguez Viorato le planteó el siguiente problema a Luis Brandon --el líder de la selección 2009:
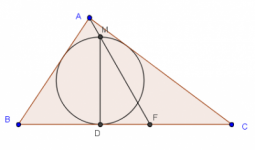
El incírculo de un triángulo $ABC$, es tangente en $D$ al lado $BC$ y $DM$ es un diámetro. El rayo $AM$ corta en $F$ el lado $BC$. Demostrar que $BD=CF$.
Homotecia en un isósceles
Considere un triángulo $ABC$ con $AB=AC$, y sea $D$ el punto medio de $BC$. La circunferencia de diámetro $AD$ corta el lado $AB$ en $B'$ y el lado $AC$ en $C'$. El circuncírculo de $ABC$, con centro en $O,$ es tangente al lado $AB$ en $P$ y al lado $AC$ en $Q$. Si llamamos $M$ al punto medio de $PQ$, demostrar:
- $B'M$ es paralelo a $BO$
- $M$ es equidistante de los lados del triángulo $AB'C'$
Dos cuerdas por el punto medio de una cuerda
Sea $AB$ una cuerda que no pasa por el centro del círculo y considere dos cuerdas $CD,EF$ que se cortan en el punto medio $P$ de $AB$. Demostrar que si las tangentes a la circunferencia en $C$ y $D$ se cortan en $Q$, y las tangentes en $E$ y $F$ se cortan en $R$, entonces $QR$ es paralela a $AB$.
Criterio para establecer cíclico con potencia de un punto
Si las rectas $AB,CD$ se cortan en $P$ y $PA\cdot{PB}=PC\cdot{PD}$, entonces los puntos $A,B,C,D$ pertenecen a una misma circunferencia. Demostrarlo.
Bisectriz, dos triángulos, circuncírculos, potencia...
La bisectriz del ángulo $B$ del triángulo $ABC$ corta a $CA$ en $D$. El circuncírculo del triángulo $BCD$ corta el lado $AB$ en $E$, y el circuncírculo del triángulo $ABD$ corta al lado $BC$ en $F$. Demostrar que $AE=CF$.
Dos homotecias en un trapecio
Las prolongaciones de los lados $AB$ y $CD$ de un trapecio se intersecan en $K$, y sus diagonales en $L$. Si $M,N$ son los puntos medios de de las bases, demostrar que los puntos $K,L,M,N$ están en una misma recta.
