Publicaciones Recientes
Una comunicación que calla: sobre el concepto de antiparalelas
Voy a ilustrar en este post la multiplicidad de conexiones que un cognizador debería establecer con una teoría previa en el momento de resolver (o estudiar la solución a) un problema de matemáticas escolares. Sostengo que la forma condensada de presentar las soluciones es una forma reticente de comunicar --así sea de manera involuntaria o por razones de estilo de redacción.
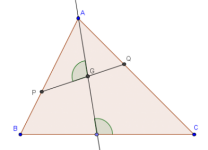
Antiparalelas
Dos rectas se dicen antiparalelas, respecto a un ángulo de referencia, si forman el mismo ángulo en lados opuestos de la bisectriz de ese ángulo.
Demostrar que:
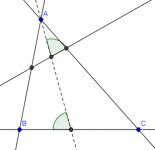
La clave está en la figura
En el triángulo $ABC$, rectángulo en $C$, la bisectriz de $A$ corta a $BC$ en $P$ y la bisectriz de $B$ corta a $CA$ en $Q$. Sean $M$ y $N$ las proyecciones de $P$ y $Q$, respectivamente, sobre el lado $AB$ . Calcular la medida del ángulo $MCN$.
El cuadrado de Polya --con Geogebra
En este post comento sobre un posible proceso de solución al problema clásico de inscribir un cuadrado en un triángulo, usando el software de geometría dinamico Geogebra.
El cuadrado de Polya
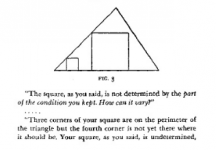
En el problem solving de las matemáticas escolares hay algunos problemas que son ya legendarios. Uno de ellos es el problema del cuadrado de Polya. Se trata de inscribir un cuadrado en un triángulo. A continuación su enunciado:
Inscribir un cuadrado en un triángulo $ABC$. Dos de los vértices del cuadrado deben estar en la base $BC$, y los otros dos en los otros dos lados, uno en cada uno.
Banda de Moebius
Tengo una duda sobre espacios infinitos: en este problema:
-En un camino infinito en ambas direcciones, el correcaminos sale a velocidad constante. Al rato sale el coyote a perseguirlo, a velocidad constante. La velocidad del correcaminos es igual al 90% de la velocidad del coyote. El coyote no sabe a qué hora salió el correcaminos y tampoco sabe en qué dirección salió. Demostrar que de todos modos el coyote puede alcanzar al correcaminos.
Como verán es bastante complicado, sobre todo porque en espacios infinitos no se cumplen las mismas reglas que en la realidad, aparte qué pasa si el correcaminos salió en infinito tiempo antes que el coyote y en dirección contraria?
Una propiedad banal de dos isogonales
Sea $ABC$ un triángulo y $\Gamma$ su circuncírculo con centro $O$. La altura de $A$ y el radio $OA$ forman un ángulo cuya medida es la diferencia de las de $B$ y $C$
Circuncentro y ortocentro: una propiedad métrica
Sean $H$ el ortocentro y $O$ el circuncentro del triángulo $ABC$. Si $M$ es el punto medio del lado $BC$, entonces $AH=2MO$. Demostrarlo.
Demostrar [paridad]
Este problema no sé cómo resolverlo. Espero que alguien me ayude:
" Se sueldan 2001 varillas (rectas) formando un camino. Demostrar que no existe ninguna línea recta $-$no pasando por un punto de soldadura del camino$-$ que intersecte a todos los 2001 segmentos del camino. "
Gracias.
Construcción de un triángulo... ¡con gestión del entusiasmo!
En este post voy a discutir la solución de un problema de construcción geométrica con regla y compás utilizando un enfoque al he llamado de entusiasmo --un poco para estar a la moda mass mediática de los libros de autoayuda y gestión del entusiasmo.
Para ilustrar el hecho de que el entusiasmo puede quedarse en el mero sueño si no es acompañado de una lógica sana, comparo mi método con los sueños de un desposeido en la canción americana "If I only had a match"
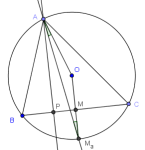
Construcción de un triángulo
Construir el triángulo $ABC$ dadas las longitudes $m_a$ de su mediana desde $A$, $d_a$ de la bisectriz del ángulo $A$, y $h_a$ de la altura del vértice $A$ (respecto a su lado opuesto $BC$).
