Publicaciones Recientes

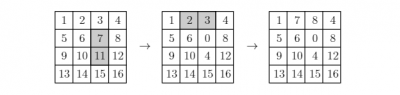
En una cuadrícula de $n \times n$ se escriben los números del 1 al $n^2$ en orden, por renglones, de manera que en el primer renglón aparecen los números del 1 al n, en el segundo los números del n+1 al 2n, y así sucesivamente. Una operación permitida en la cuadrícula consiste en escoger cualesquiera dos cuadraditos que compartan un lado y sumar (o restar) el mismo número entero a los dos números que aparecen esos dos cuadraditos. Por ejemplo, aquí abajo se muestran dos operaciones sucesivas permitidas en una cuadrícula de 4x4: primero restando 7 a los cuadraditos sombreados y luego sumando 5 a los sombreados.

Encuentra el menor número real $x$ que cumpla todas las siguientes desigualdades: 

$$\lfloor x \rfloor < \lfloor x^2 \rfloor <  \lfloor x^3 \rfloor < \dots < \lfloor x^n \rfloor < \lfloor x^{n+1} \rfloor < \dots$$

Nota: $\lfloor x \rfloor$ es el mayor entero menor o igual a $x$, es decir, es el único número entero que cumple que $\lfloor x \rfloor \leq x < \lfloor x \rfloor + 1$. 

Sean $\mathcal{C}_1$ y $\mathcal{C}_2$ dos circunferencias tangentes externamente en $S$ tales que el radio de $\mathcal{C}_2$ es el triple del radio de $\mathcal{C}_1$. Sea $l$ una recta que es tangente a $\mathcal{C}_1$ en $P$ y tangente a $\mathcal{C}_2$ en $Q$, con $P$ y $Q$ distintos de $S$. Sea $T$ el punto en $\mathcal{C}_2$ tal que $TQ$ es diámetro de $\mathcal{C}_2$ y sea $R$ la intersección de la bisectriz de $\angle SQT$ con el segmento $ST$. Demuestra que $QR = RT$

Un entero positivo $N$ es norteño si para cada dígito $d >0$, existe un divisor de $N$ cuyo último dígito es $d$. ¿Cuántos números norteños menores que 2016 hay que tengan la menor cantidad posible de divisores?