Publicaciones Recientes
Problema 2 BMO 2009
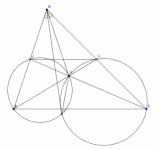
Sea MN una línea paralela al lado BC del triángulo ABC, con M sobre el lado AB y N sobre el lado AC. Las íineas BN y CM se intersectan en un punto P. Los circuncírculos de los triángulos BPM y CPN se intersectan en P y Q. Demostrar que ∠BAQ=∠CAP
Otro de un cuadrado, dentro de otro cuadrado.
Sea ABCD un cuadrado de centro O. Sean P, Q, R y S puntos en DA, AB, BC y CD, repectivamente, tales que P,O y R son colineales; y Q, O y S también lo son (colineales), y de manera que PR es perpendicular a QS. Demostrar que el cuadrilátero PQRS es un cuadrado.
L1.P23 (Un clásico --para terminar la lista)
Encontrar todas las soluciones en enteros positivos de la ecuación 1/x+1/y+1/z=1.
L1.P22 (Una ecuación cuadrática)
La ecuación x2+bx+2=0 tiene solamente una raíz. Determinar los valores de b.
L1.P21 (Cuadrado en el centro de un cuadrado)
Los puntos medios L,M,N,O de los lados QR,RS,SP,PQ de un cuadrado PQRS se unen con con un segmento de recta a los vértices de éste de manera que se forme un cuadrado P′Q′R′S′. Calcular la razón de áreas de los dos cuadrados.
L1.P20 (2009 como suma de impares)
El número 2009 se puede expresar como suma de n enteros impares consecutivos (n≥2) en varias formas. ¿Cuál es el menor valor posible de n?
L1.P19 (Doblez)
Un triángulo rectángulo isósceles, con lados iguales de medida 2, ha sido recortado de una hoja de papel que es gris de un lado y cuadriculada del otro.
L1.P18 (Producto de 3 dígitos)
¿Cuántos números abc de tres dígitos son tales que al multiplicar los dígitos se obtiene un producto mayor que 60 pero menor que 65?
L1.P17 (Galletas de chocolate y almendras)
Un lote de galletas contiene galletas con almendras, galletas con chocolate, galletas con los dos ingredientes y otras que no contienen ninguno de los dos. Se encontró que 3/10 tienen almendras, 1/2 tienen chocolate y 3/28 tienen ambos ingredientes. Sin embargo se encontró que 172 galletas no tienen ninguno de los dos ingredientes.
L1.P16 (Piso enmosaicado)
Un piso rectangular está cubierto de mosaicos cuadrados. Tomando como unidad de longitud el lado de un mosaico, el piso tiene dimensiones 45 de largo y 20 de ancho. Si se traza una diagonal de una esquina a la opuesta del piso ¿cuántos mosaicos cruza la diagonal?
