Publicaciones Recientes
Reto para novicios: el problema 4 de la IMO 2009 (invertido y con 4 incisos)
Aprovechando el entusiasmo de Brandon voy a poner aquí una variante del problema 4 de la IMO 2009, desglosándolo e invirtiéndolo con la idea de reducir su complejidad. Pero antes de plantear el reto a los miembros de la preselección Tamaulipas 2009, permítaseme comentar dos o tres cosas sobre ese problema, sobre su dificultad.
IMO 2009: México en el lugar 50
Según los datos en el sitio http://imo-official.org/results.aspx, México se colocó en la L IMO en el lugar 50. El primer lugar lo ocupó China y el último (104) Argelia. La delegación mexicana obtuvo 74 puntos, la china 221 y la argelina 2.
Problema 5(N)
El alumno menos aventajado del salón canceló el 6 en 16/64 y obtuvo 1/4 --la respuesta correcta. Encontrar todos los pares de números de dos cifras ab, bc tales que ab/bc=a/c --con a,b,c dígitos diferentes. (Es decir, todos los casos en que este alumno podría acertar con su método al simplificar quebrados de dos cifras.)
IMO 2009 Problema 1
Sea n un entero positivo y sean a1,a2,...,ak(k≥2) enteros distintos del conjunto 1,...,n, tales que n divide a ai(ai+1−1), para i=1,...,k−1. Demostrar que n no divide a ak(a1−1).
IMO 2009 Problema 2
Sean ABC un triángulo de circuncentro O, P y Q puntos sobre AB y AC, respectivamente, y K, L, M los puntos medios de BQ, CP y PQ, respectivamente. Si el circuncírculo del triangulo KLM es tangente a PQ, demostrar que OP=OQ.
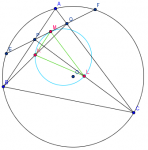
IMO 2009 Problema 4
En un triángulo ABC, donde AB=AC, los bisectrices internas de ∠A y ∠B cortan a los lados BC y AC en D y E, respectivamente. Sea I el incentro del triángulo ADC. Supongamos que ∠IEB=45. Encontrar todos los valores posibles de ∠A.

Probar isósceles
En una semicircuferenica de diámetro AB se elige un punto D y se baja una perpendicular al diámetro AB cortándolo en C. En el espacio descrito por DC, CB y el arco BD se inscribe un círculo tangente a CD en L, a BC en J y al arco BD en K. Demostrar que AD=AJ.
Encontrar el término n de una sucesión
Considere la sucesión a1=1 y, para n mayor que 1, an=1+2an−1. Encontrar una fórmula para el término n-ésimo y demostrarla por inducción.
Saltillo 2007
Fotos de la Olimpiada Mexicana de Matemáticas celebrada en saltillo de 2007. Por la selección de tamaulipas.
