Publicaciones Recientes
Mesas circulares!
Hay 3 equipos, cada uno de ellos con 3 personas. Se quieren sentar alrededor de una mesa redonda con sillas numeradas del 1 al 9. ¿De cuantas formas se pueden sentar las 9 personas en las sillas, de tal manera que cualesquiera dos personas consecutivas del mismo equipo esten separados entre si por la misma cantidad de sillas?
Numeros enteros positivos
Demuestre que sin importar que numeros enteros naturales sean m y n, el numero mn(m+n)(m−n) es divisible por 3.
11 ONMAS Guerrero
ABCD es un cuadrado, el punto E esta en el lado BC. BD y AE se intersectan en el punto F. Con centro en el punto F y radio FA se traza una circunferencia que intersecta al lado CD en el punto G. Calcula el valor del angulo GFE y demuestra que el triangulo GFC es isisceles.
Problema de la X ONMAS
Utilizando los números 1,2,3,4,5,6,7,8,9 se quieren armar conjuntos que tengan dos o mas de esos números, sin repetición, de modo que si se multiplican todos los números del conjunto, el resultado que se obtiene es múltiplo de 4 pero no es múltiplo de 8.
¿Cuántos de estos conjuntos se pueden armar ?
Teorema de la altura: una prueba visual
En nuestra sociedad globalizada, en la que el espectáculo y la diversión han sido puestos en el centro por los mass media, es muy difícil ser profesor, de cualquier cosa, pero sobre todo de matemáticas. ¿Tiene que ser convertida el aula en un reality show para atraer la atención de nuestros estudiantes?
Resultados del selectivo final... y selección OMM_Tam_2011
Para los resultados del examen selectivo final atacho el archivo. La selección es la siguiente:
Bernardo Antonio Tovías Guerrero 64
Luis Germán Díaz Zúñiga 51
Claudia Lorena Cabrera Arjona 46
José Enrique Olvera Vázquez 44
Alma Rosa Meléndez Martínez 32
Alejandra Echavarría Gallegos 31
Felicidades y ¡vamonos recio por dos platas y dos bronces!
Los saluda
jmd
Nietzsche, el nihilismo --y la reducción al absurdo
El último jueves del mes pasado ofrecí una charla sobre Nietzsche en la UAMCEH_UAT dentro del seminario de filosofía denominado Café y Rollos. Atacho el texto en que basé la presentación. Está en forma de cuadernillo, es decir, hay que imprimir a doble cara y después doblar a la mitad.
La parte de la charla que podría ser de interés para los lectores de MaTeTaM es la que presento en este post. Presenta el método de prueba de la reducción al absurdo con un trasfondo nihilista. Me sirvió para mostrar el lado no negativo de Nietzsche y el Nihilismo.
Problemas y resultados del V selectivo (OMM_Tam_2011)
Enseguida se presentan los problemas del quinto examen selectivo y los puntajes que los preseleccionados obtuvieron en él.
1.- Sean A,B,C,D,E,F,G,H,I 9 puntos distintos en una circunferencia de radio r, de tal manera que ABCD es un cuadrado y EFGHI es un pentágono regular. Demuestra que hay un arco cuya longitud es no mayor que πr20.
2. Sean a,b,c 3 números enteros positivos con (a,b)=k y 5a2a+b=kc. Encuentra los posibles valores de c.
Sobre el concepto de frónesis en el problem solving
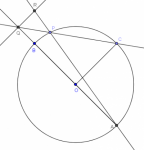
Cuarto examen selectivo OMM_Tam_2011
1. Sean AB un diámetro de una circunferencia con centro en O, y C un punto sobre ella de manera tal que OC y AB son perpendiculares. Considere un punto P sobre el arco BC. Sean Q la intersección de las rectas CP y AB, y R la intersección de la recta AP con la recta perpendicular a AB que pasa por Q. Demostrar que BQ=RQ.
2. Determina el mayor entero positivo n para el cual existe una reordenación a,b,c,d de los números 3,6,9,12 de manera que
n√3a×6b×9c×12d
es un entero.
