Básico
Trivial --pero no para el novicio
Demostrar que $n^2-1$ es múltiplo de 8 para cualquier $ n $ impar no negativo.
Problema 1, ONMAS 2008
¿Cuántos divisores cuadrados perfectos tiene el número $ 2008^{2008} $ ?
Diez cajas de billar y una báscula electrónica.
Tenemos 10 cajas con bolas de billar; cada caja pesa 10kg y contiene 10 bolas de billar (1kg cada una). Pero, una de las cajas salió defectuosa, aunque todas sus bolas pesan lo mismo, la caja completa pesa 9kg. Es decir, en una de las cajas, todas la bolas pesan 900 gramos.
Doce bolas y tres pesadas
Determinar, con el auxilio de una balanza y en sólo tres pesadas, una bola de entre doce, que pesa distinto a las demás. Además, determinar si la bola pesa más o menos que las otras.
Yoga de leche
Una yoga de 5 litros está llena de leche. Dos botellas vacías de 2 y 3 litros respectivamente están disponibles para transferir el líquido entre las botellas y la yoga de 5 litros. Exhibir un procedimiento para lograr 4 litros de leche en la yoga de 5 litros. Encontrar una sucesión de transferencias de leche de longitud 3.
Las cervezas de Bart Simpson
Bart Simpson cuenta, usando sus dedos de la mano derecha, las cervezas que se ha tomado su papá en la semana. Si cuenta empezando con el meñique y termina en el índice pulgar y vuelve a empezar con el meñique, y contó 777 ¿en qué dedo terminó la cuenta? (Nota: Bart solamente tiene 4 dedos. Además, hay que suponer que sabe contar hasta 777...) ¿En qué dedo terminaría si tuviese 5 dedos?

Ángulos en el reloj
¿Cuál es el ángulo que forman las manecillas del reloj a las 9:30? (Argumento fiador requerido.)
Tres círculos congruentes
Tres círculos $C_1, C_2, C_3$ del mismo radio se intersectan no tangencialmente en un punto $P$. Sean $A, B$ los centros de $C_1, C_2$, respectivamente; y $C, D$ los puntos de intersección de $C_1, C_2$, respectivamente, con $C_3$. ($C, D$ son ambos diferentes de $P$.) Demostrar que $ABCD$ es un paralelogramo.
Interrupción de la filosofía --en Tijuana
Alejandra (de 37 abriles) fue apañada por un retén de la PGR en Tijuana, el día último de abril, apenas cruzó la aduana procedente de San Diego. Le incautaron 30000 US Dollars, producto de la recaudación por venta de coca en USA.
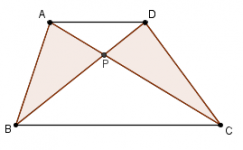
Áreas iguales en un trapecio
Demuestra que para cualquier trapecio ABCD, las áreas de las triángulos sombreados son iguales.