Municipal OMM Tamaulipas 2010
Problema 5 (Ciudades, OMM_Tam_2010)
Con los dígitos 1,2,…,9 ¿Cuántos números de tres cifras distintas se pueden formar, con la condición de que la suma de sus cifras sea par?
Problema 7 (Ciudades, OMM_Tam_2010)
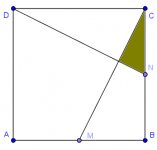
Sea ABCD un cuadrado con lado 1 cm. Si M y N son los puntos medios de los lados AB y BC, respectivamente. Calcular el área de la zona sombrada.
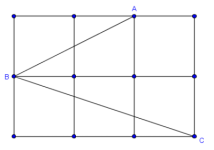
Problema 4 (Ciudades, OMM_Tam_2010)
La figura muestra una cuadrícula formada por 6 cuadrados. ¿Cuanto mide el ángulo CBA?
Problema 5
Cuantos números de 3 cifras, que la suma de sus cifras sea par se pueden formar con los digitos 1,2,3...9
Problema 10 (Ciudades, OMM_Tam_2010)
Si una alberca se llena usando 2 mangueras de diferente tamaño en 4 horas, y la manguera chica se tarda 6 horas más que la grande en llenar la alberca cuando se usa sola. ¿Cuanto tiempo se tarde la manguera chica en llenar la alberca?
Problema 8 (Ciudades, OMM_Tam_2010)
Hallar un número de tres cifras ab6 sabiendo que las tres últimas cifras de (ab6)2 son ab6.
Problema 3 (Ciudades, OMM_Tam_2010)
Dos números enteros consecutivos son tales que la mitad del menor más el mayor, excede en 13 a 1/5 del menor más 1/11 del mayor.
Problema 9 (Ciudades, OMM_Tam_2010)
Problema 2 (Ciudades, OMM_Tam_2010)
Probar que el número abcabc es múltiplo de 7, de 11 y de 13.
Problema 1 (Ciudades, OMM_Tam_2010)
Carlos tiene un cierto número de monedas de colección. Cuando ordena las monedas en montones de 5, no le sobra ninguna moneda. Cuando las ordena en montones de a 6, tampoco le sobran monedas. Pero si las ordena en montones de 7, le sobra una moneda. ¿Cuál es el menor número de monedas que puede tener Carlos?
