Asumamos primero que es posible triangular al pentágono de tal manera que los triángulos tienen sus vértices en los 1000 puntos y que no hay dos triángulos traslapados.
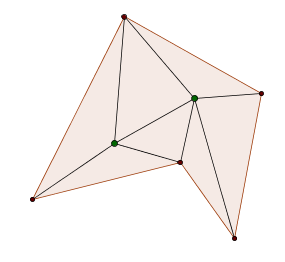
La figura muestra un ejemplo de éste tipo de triangulaciones en un pentágono con dos puntos dentro (puntos verdes).
Una vez que creemos que podemos triángular al pentágono con sus 995 puntos dentro, entonces lo que resta es calcular cuántos triángulos hay en la triangulación. Para ello calcularemos la suma de los ángulos internos de los triángulos de dos formas distintas:
1. La suma de los ángulos internos de todos los triángulos es 180\codtn donde n es el número de triángulos.
2. Por otro lado, esta suma es igual a sumar los ángulos internos del pentágono ( 180∘×3=540∘ grados) más la suma de los ángulos alrededor de cada uno de los puntos internos, esto es, 360° grados por cada vértice.
En consecuencia, obetenemos que:
180\codtn=540+360×995
Despejando n de esta ecuación se obtiene que n=1993. De aquí se concluye que la triangulación debe constar de 1993 triángulos y como el área es 1993, debe haber un triángulo con al menos área 1. Entonces sólo resta demostrar la existencia de la triangulación.
Existencia de la triángulación.
Esta parte la dejaré pendiente pues creo que debe ir como teorema.

Brandon Este problema es para
Brandon
Este problema es para que vayas practicando Geometría-Combinatoria, es un tema que cada vez se ve más en la OMM. Te sugiero que vayas resolviendo este tipo de problemas, pues los de geometría ya los tienes dominados.
Números complejos, proyectividades, ejes radicales, polos y polares son temas que revazan por mucho los temas actuales de la Olimpiada Mexicana de Matemáticas. No está demás aprenderlos, pero está mal no aprender de lo demás.
Jesus, lo hice sin realizar
Jesus, lo hice sin realizar calculos en una figura asi que espero y este bien.
Consideremos la envolvete convexa de 5 puntos(el pentagono), es claro que existen 995 puntos dentro de esta. Por otro lado la suma de los angulos internos del pentagono es 3(180).
Y en cada punto dentro podemos asumir que tenemos 360 grados de ahi la suma de todos los angulos de los puntos internos es 995(360). De ahi sumando tenemos que la suma de los angulos es:
3(180)+995(360)=358560=1993(180), es decir se pueden formar 1993 triangulos, de ahi lo pedido es evidente.
Espero y este entendible, la primera parte fue de un problema que ya habia realizado, que es considerando una envolvente convexa de n puntos, en la cual hay p puntos dentro, determina la cantidad de triangulos que se pueden formar.
Espero y este bien y comprensible. Saludos!!!y empesare a ver mas a fondo geometria convinatoria
No entiendo bien porqué
No entiendo bien porqué consideraste la envolvente convexa del pentágono, pues ya estaba dado que era un pentágono y que tenía 995 puntos dentro. Ojalá me pudieras explicar esa idea.
Por otro lado, tienes todos los argumentos necesarios para dar la prueba, pero creo que te hace falta claridad. Dijiste que la suma de los ángulos internos de un pentágono más 360*995 dividido entre 180 es 1993 y que eso, por alguna razón que no mencionas, implica que se pueden formar 1993 triángulos. Me parece que hace falta explicar cómo tus cuentas implican que hay 1993 triángulos. Estoy seguro que lo sabes, pero sin duda te hizo falta explicarlo.
De cualquier manera, ya metí en la solución el argumento completo. Y no te preocupes mucho por este comentario, si fuera la Olimpiada Nacional, con lo que dejaste escrito yo me encargo de sacar los 7 puntos. Aunque, claro, me ahorrarías una discusión si estuviera más claro.
Saludos
Se no estaba muy claro, a lo
Se no estaba muy claro, a lo que me referia es que cada punto punto dentro del pentagono lo podiamos usar como vertice de un triangulo de ahi lo que conte cada punto como 360 grados, ya que sumando los internos del pentagono podemos obtener cuanto suman todos los angulos y de ahi sacar cual es el maximo de triangulos en el que podemos dividir el pentagono. Pero sin duda si me falto aclarar eso, como mencionas, creo que ahora detallare mas en mis demostraciones escribiendo a bien todas las ideas.
Gracias Jesus, estare estudiando un material de Geometria Convinatoria que me dejo el profesor Muñoz, cabe mencionar que cuando me lo dio no le entendia muy bien pero eso ya quedo atras, saludos!!!y gracias!!!
haha que genial era el
haha que genial era el problema 3 no lo habia notado...mmm pero es de 1993...se supone que cada año es mas dificil no?...saludos y ya vi el problema de la ibero te pondre una solucion esperando que este del todo bien saludos