Problemas - Teoría de números
Tabla con números sin 3 o 7
2.4. Se tiene una tabla con siete columnas A,B,C,D,E,F,G y se coloca en ella los números naturales que no contienen al 3 o al 7 en su desarrollo decimal. Se empieza en la casilla C1, como se muestra. ¿En cuál columna y renglón queda el 2014?

Espiral con el 2014 en cuadrícula
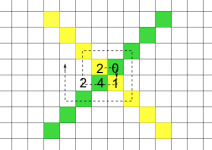
2.3. Sobre una cuadrícula se coloca 2014 veces el número 2014 (un dígito en cada casilla) siguiendo una espiral como se muestra en la figura. Sea M la suma de los números sobre las casillas verdes y N la suma de los números sobre las casillas amarillas. Calcula la diferencia entre M y N.
La lista de Julio
1.4. Julio hace una lista con los números que cumplen las siguientes condiciones:
--El número es de ocho cifras, todas diferentes.
--Es múltiplo de 8.
--Cada dos cifras adyacentes en el número forman un nuevo número que es múltiplo de 7 o de 13, aunque no necesariamente todos múltiplos del mismo número.
Encuentra los números de la lista de Julio.
Números mazatlecos
1.2. Se dice que un número de cuatro cifras diferentes entre sí y distintas de cero es Mazatleco si al eliminar la mayor y la menor de las cifras, las dos restantes suman 10. ¿Cuántos números Mazatlecos hay?
Llevar o no llevar: that's the question
1.1. Se forman tres números enteros de tres cifras, abc,def,ghi, donde cada letra representa un dígito del 1 al 9 sin que se repitan. Si la suma de los tres números termina en 65 ¿cuál es el valor de dicha suma?
Ejercicio en matemáticas del reloj
Recuerdos de Querétaro 1998
Encontrar los enteros positivos mínimo (m) y máximo (M) que se pueden expresar en la forma $1/a_1+2/a_2+3/a_3+...+9/a_9$ (Donde $a_1,...,a_9$ son dígitos, no necesariamente distintos.)
Suertudos
Un número se dice que es suertudo si al sumar los cuadrados de sus cifras y repetir esta operación suficientes veces se obtiene el número 1. Por ejemplo el número 1900 es suertudo, pues en la primera operación se obtiene 82, en la segunda 64+4=68, en la tercera se obtiene 100 y en la cuarta se obtiene el 1. Encontrar dos números consecutivos que sean suertudos.
3m+2 nunca es cuadrado perfecto
Sea m un entero. ¿Puede ser cuadrado perfecto un número de la forma 3m+2?
Cuadrado mágico inconcluso
Los números del 1 al 16 se colocan en una cuadrícula de 4 por 4 de manera que la suma por columnas, por filas y por diagonal es la misma. En la siguiente cuadrícula solamente algunas casillas se han llenado. Termina de llenarla.
__ __ 3 16
__ 15 __ 5
14 __ 8 11
7 12 13 __
