Publicaciones Recientes
Resultados del segundo examen selectivo
Los primeros 16 de la siguiente tabla son los preseleccionados que permanecen. Las gracias les sean dadas a todos los participantes por apostar su tiempo y esfuerzo en favor de las matemáticas.
Puntajes en el segundo selectivo
Una diofantina muy difícil
Resolver la ecuación diofantina siguiente para enteros no negativos x,y,z:
$$x^2+y^4+z^6=2^{1111}$$
Inferencias de paridad
Sea $n\geq2$ un entero. Los números $x_1,x_2,\ldots,x_n$ son elementos del conjunto $\{-1,1\}$ y cumplen la ecuación $x_1x_2+x_2x_3+\ldots+x_nx_1=0$. Demostrar que $ n $ es múltiplo de 4.
Adictos al Xbox
Los adolescentes de una preselección olímpica de matemáticas tienen una actividad de entretenimiento favorita: 17 son adictos al Xbox (conjunto A1), 13 a las series americanas de TV (A2), 8 a la resolución de problemas de concurso (A3), y 6 no tienen actividad recreativa conocida.
Pudorosa (segunda parte)
Decidir --con prueba-- si la ecuación diofantina $123x+426y=8$ tiene solución.
Una pudorosa propiedad del máximo común divisor
Si $a, b$ son enteros y cumplen $7a-38b=-2$ ¿qué se puede concluir sobre el máximo común divisor de a y b?
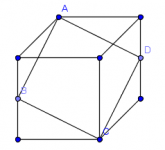
Cuadrilátero en un cubo
En un cubo de arista 6 los puntos medios B,D de dos aristas opuestas, y dos vértices opuestos A,C pero no en las aristas de los puntos medios B,D, forman un cuadrilátero ABCD. Encontrar el área de ese cuadrilátero.
¿Es múltiplo de 11? (Que lo diga Fermat.)
Decidir --con prueba-- si $61^{61}+71^{71}$ es divisible entre 11.
ExSel2_Pr1: Inclusión y exclusión... pero basta con razonarlo
¿Cuántos números enteros positivos no mayores que 1000 no son ni cuadrados ni cubos?
Elemental,... pero sólo si sabes usar el PTF
Encontrar todos los primos $q$ tales que $4+2^q$ es múltiplo de $2q.$
