Publicaciones Recientes
División anular
Sean $a, b, c$ tres números enteros positivos tales que $a$ divide a $b^2$, $b$ divide a $c^2$ y $c$ divide a $a^2$. Demostrar que $abc$ divide a $a^7+b^7+c^7$.
Tres círculos congruentes
Tres círculos $C_1, C_2, C_3$ del mismo radio se intersectan no tangencialmente en un punto $P$. Sean $A, B$ los centros de $C_1, C_2$, respectivamente; y $C, D$ los puntos de intersección de $C_1, C_2$, respectivamente, con $C_3$. ($C, D$ son ambos diferentes de $P$.) Demostrar que $ABCD$ es un paralelogramo.
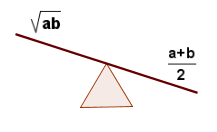
Desigualdad de las medias --con un max-min-razonamiento
¿Qué teoremas se valen de conjugados armónicos en la olimpiada?
Brandon me comentó en el problema "Bisectriz, ángulo recto y conjugados armónicos" lo siguiente:
Interrupción de la filosofía --en Tijuana
Alejandra (de 37 abriles) fue apañada por un retén de la PGR en Tijuana, el día último de abril, apenas cruzó la aduana procedente de San Diego. Le incautaron 30000 US Dollars, producto de la recaudación por venta de coca en USA.
Tutorial: Cómo poner imágenes desde un servidor en comentarios de MaTeTaM
La mayoría de nosotros sabemos cómo subir imágenes a un servidor externo y poner imágenes (principalmente de geometría) en nuestros comentarios. A los que estén interesados, este pequeño tutorial se trata de cómo subir nuestras imágenes a un servidor para luego poder ponerlas en MaTeTaM.
Una factorización notable (en la IMO 69)
Demuestre que existen infinitos $ m $ enteros positivos tales que $n^4 + m$ es un número compuesto para cualquier $ n $ entero positivo.
Una factorización notable
Encontrar todos los enteros $ n $ tales que $n^4+4$ es primo.
Producto del máximo y el mínimo
Hallar el producto del máximo y el mínimo valor de (3x+1)/(9x^2+6x+2)
Saludos.
León-Sotelo.
Cíclico en tres circunferencias tangentes
Considere $\mathcal{C}_1$, $\mathcal{C}_2$ y $\mathcal{C}_3$ tres circunferencia que por pares son tangentes externas. Llamemos $P$ y $Q$ los puntos de tangencia de $\mathcal{C}_1$ con $\mathcal{C}_2$ y $\mathcal{C}_3$ respectivamente.
