Publicaciones Recientes
Razonamiento diagramático en problemas verbales
7 divide a todos
Inferencias a partir de la relación de divisibilidad
Resolver (en números enteros positivos) el siguiente sistema de ecuaciones
$a^3-b^3-c^3=3abc$
$a^2=2(b+c)$
Más allá de los datos: inferencias elementales en un problema básico de números
Encontrar todas las soluciones en enteros positivos de la ecuación $8x+3y+2z=18$.
Perpendiculares
Para un triángulo $ ABC $, toma los puntos $ M $ y $ N $ en las extensiones de AB y CB, respectivamente de tal manera que $ M $ y $ N $ estén más cerca de $ B $ que de $ A $ y $ C $, y que $ AM=CN=s $ donde $ s $ denota el semiperímetro. Sea $ K$ el punto diametralmente opuesto a $ B $ e $ I $ el incentro del triángulo $ ABC $.
Midas en México... y con padrinos
Un empresario tiene que distribuir todas sus ganancias de los siguientes tres meses entre tres padrinos (después de eso queda liberado de los favores recibidos en forma de contratos).
Equilátero inscrito en equilátero
Inscribir un triángulo equilátero en un triángulo equilátero $ ABC $, de tal manera que cada lado del inscrito sea perpendicular a un lado del triángulo $ ABC $. (Describir el procedimiento de construcción.)
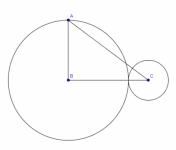
Problema 6G, Ciudades 2009
En la figura el segmento $ BC $ une los centros de los círculos tangentes, $AB$ es perpendicular a $BC, BC =8$ , y $AC =10$. Calcular el área de cada círculo.
¿Incírculo o excírculo?
Sean $D$ en $AB$ y $E$ en $AC$, los extremos de un segmento tangente al incírculo del triángulo $ ABC $. Si los lados $AB, BC, CA$ miden, respectivamente, $c, a, b$, expresar el perímetro del triángulo ADE en términos de $a, b, c$.
Selecciones Reynosa y Victoria
Quedaron integradas otras dos selecciones de la etapa Municipal de la XXIII OMM tamaulipeca: Reynosa y Victoria.

