Publicaciones Recientes
Ternas Pitagóricas (parte 3)
Demostrar que en cualquier terna pitagórica primitiva a2+b2=c2, exactamente dos de los números a,b,c son impares. (Primitiva significa sin divisores en común.)
Ternas Pitagóricas (parte 2)
Demostrar que en cualquier terna pitagórica a2+b2=c2, al menos uno de los números a, b, c es divisible entre 5.
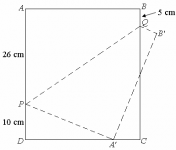
Geometría con origami
Una hoja de papel en forma rectangular ABCD se dobla a lo largo de la línea PQ de manera que el vértice A quede en el lugar del punto A′ y el vértice B en el lugar del punto B′. Al medir los segmentos AP,BQ,DP, se tiene que miden 26cm,5cm y 10cm, respectivamente.
¿Cuál es el área del la hoja de papel?
Problema 6, ONMAS 5 (modificado)
En un rectángulo de base 10 y altura 8, se ha inscrito un paralelogramo de tal manera que en las esquinas del rectángulo se forman triángulos de catetos 4 y 7 y 3 y 4. Encuentra la distancia entre los lados opuestos del paralelogramo inscrito en el rectángulo.
La selección de la ONMAS tamaulipeca se mantiene en stand by
En la siguiente lista de adolescentes victorenses se encuentran (con probabilidad 1) los 6 que integrarán la selección tamaulipeca de la Olimpiada Nacional para Alumnos de Secundaria
Hábitos de la mente (para el desempeño eficaz )

Problema 6 OMM 2003
Dado un entero n un cambio sensato consiste en sustituir n por 2n+1 ó 3n+2. Dos enteros positivos a y b se llaman compatibles si existe un entero que se puede obtener haciendo uno o más cambios sensatos, tanto a partir de a, como a partir de b. Encuentra todos los enteros positivos compatibles con 2003 menores que 2003.
Problema 4 OMM 2003
Sea ABCD un trapecio con AB paralelo a DC. Se toman puntos P y Q sobre AB y CD respectivamente, tales que APPB=DQQC. Sea M la intersección de AQ con DP y sea N la intersección de PC con QB. Pruebe que la longitud de MN depende sólo de las longitudes de AB y DC y calcula su valor.
Ciencias blandas (Soft science)
Tres licenciados en ciencias blandas han tenido que entrar al mercado laboral con sus habilidades preuniversitarias. Con la siguiente información decide en qué trabaja cada uno.
Triángulos de igual área
Demostrar que un cuadrilátero es paralelogramo si y sólo si cada una de sus diagonales lo divide en dos triángulos de igual área.
