Publicaciones Recientes
Isogonales: iso (igual) gono (ángulo)
Demostrar que, en un triángulo $ABC$, la altura de cualquier vértice y la recta que pasa por él y el circuncentro forman el mismo ángulo con la bisectriz (de ese mismo vértice).
Reflejos en el espejo de la bisectiz
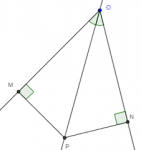
Dentro del triángulo $ABC$, considere un punto $P$, y $C'$ y $B'$, los pies de las perpendiculares bajadas desde $P$ a los lados $AB$ y AC, respectivamente. Demostrar que si $Q$ es un punto tal que $C'PB'Q$ es paralelogramo, entonces las rectas $AP$ y $AQ$ son simétricas respecto a la bisectriz del ángulo $A$.
Dualidad en geometría
Tres vecinas
A: Al departamento de al lado se acaban de cambiar tres mujeres -según me lo dijo C.
Regla del 41 para ninis
En el país XYZ se aprobó una ley de "jubilación" de ninis (jóvenes que ni estudian ni trabajan). Básicamente, la regla para la "jubilación" es que el joven nini recibirá una pensión estatal de tres salarios mínimos de por vida si sigue siendo joven (menos de 30) y su edad más los años que se ha mantenido nini (sin estudiar ni trabajar) es al menos 41 años. Calcular la edad en que un adolescente de 19 años logrará la pensión si tiene 4 años de nini.
Volumen de una alberca
Una alberca, cuyo espejo del agua es un rectángulo $a\times{b}$, tiene el fondo inclinado también rectangular de manera que la profundidad en un extremo ($h$) es un metro menor que la del otro. Obtener una fórmula para calcular la capacidad de la alberca en metros cúbicos y usarla para $h=1,a=3,b=6$. Nota: puedes suponer que $a,b,h$ están expresadas en metros y las paredes son verticales.
Triángulo rectángulo
El área de un triángulo rectángulo es 150 unidades, y la altura perpendicular a la hipotenusa mide 12. Calcular la longitud de sus lados.
Ficciones matemáticas
Demostrar que un cuadrilátero es paralelogramo (Problema 5, OIM)
En un triángulo acutángulo ABC sean AE y BF dos alturas, y sea H el ortocentro. La recta simétrica de AE respecto de la bisectriz (interior) del ángulo en A y la recta simétrica de BF respecto de la bisectriz (interior) del ángulo en B se intersecan en un punto O. Las rectas AE y AO cortan por segunda vez a la circunferencia circunscrita al triángulo ABC en los puntos M y N, respectivamente.
Sean: P, la intersección de BC con HN; R, la intersección de BC con OM; y S, la intersección de HR con OP.
Demostrar que AHSO es un paralelogramo.
