Publicaciones Recientes
Residuo de un factorial (módulo un primo)
Encontrar el residuo que deja 50(50!) al dividirlo entre 53.
Inverso (mod 151) de una potencia de 2
Encontrar un número entero positivo que al multiplicarlo por 2145 y al resultado restarle 1, se obtenga un múltiplo de 151.
Expresable como combinación lineal
Decidir (con justificación) cuál de los tres números 2007,2008,2009 podría ser expresado como una combinación lineal entera de 453 y 408, es decir, en la forma 453x+408y, con x,y enteros.
Encontrar un residuo
Encontrar el residuo que deja 20092008 al dividirlo entre 9
El polo de la recta que pasa por el vértice y el punto de tangencia.
Sea ABC un triángulo y sean D, E y F los puntos donde la circunferencia circunscrita es tangente al lado BC, CA y AB. Llamemos D′ el punto donde la recta EF corta a la recta AB. Demuestra que:
a) D′ es el conjugado armónico de D con respecto al segmento AB.
b) Que la recta AD es la polar de D′ respecto al incírculo.
Demostrar cuadrado
Sea ABCD un cuadrilatero tal que los angulos internos en los vertices A, B, y C son de cuarenta y cinco grados. Demostrar que los puntos medios de los lados del cuadrilatero determinan un cuadrado.
Propuesto por: Fernando
Clasificación de primos que dividen a un cuadrado más uno
Demuestra que si p es un primo impar que divide a n2+1 para algún n, entonces p debe ser de la forma 4k+1, es decir, p≡1 (mód 4).
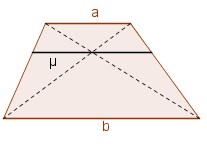
Media armónica de las bases de un trapecio.
Considere μ un segmento paralelo a las bases a y b de un trapecio, de tal manera que μ pasa por el punto de intersección de las diagonales y sus extremos están sobre los lados del trapecio. Demostrar que μ es la media armónica de a y b, es decir:
No es un cuadrado perfecto
Demostrar que si y es un entero, 187y−1 no es un cuadrado perfecto.
¿Cómo subir imágenes a MaTeTaM?
