Publicaciones Recientes
División en casos
Encontrar todas las tripletas (p,q,r) de números primos tales que pq+pr es un cuadrado perfecto.
Criba modular
Encontrar todas las soluciones (x,y) en enteros positivos para la ecuación 7x−3⋅2y=1.
La preselección se reduce a 21
El día de hoy, sábado 15 de agosto, se aplicó el primer examen selectivo, de acuerdo a programa. Enseguida se presentan los puntajes obtenidos por los preseleccionados de la Delegación Tamaulipas 2009, en el primer examen selectivo. Con este selectivo la preselección se reduce a 21 alumnos.
Múltiplo de 11 compuesto de unos
Sea p un un entero positivo. El número 11p está compuesto de m dígitos todos iguales a 1. Encontrar todos los valores de m para los cuales p es primo.
Áreas enteras de triángulos
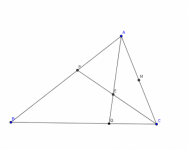
El área del triángulo ABC es un entero. Sobre los lados BC y AC se eligen los puintos X y Y, respectivamente. Los segmentos AX y BY se cortan en un punto P dentro del triángulo ABC. El área de BPX es 1, la de APY es 2, y la de APB es un entero. Encontrar el área del triángulo ABC.
Biblioteca
En mi biblioteca hay 5 libros de álgebra, 6 de combinatoria, y 8 de geometría, y todos son diferentes.
a) ¿De cuántas formas puedo elegir dos?
b) ¿De cuántas formas puedo elegir dos del mismo tema?
c) ¿De cuántas formas puedo elegir dos pero que no sean del mismo tema?
Partir la baraja
Sea n un entero positivo. Una baraja de 2n cartas contiene exactamente dos cartas marcadas con cada uno de los enteros 1,2,…,n. Las cartas se ordenan en la forma 1,1,2,2,3,3,...,n,n. La baraja ya ordenada de esta manera se parte, y resulta que, en las dos partes, los dígitos en las cartas suman la misma cantidad.
Primer selectivo el sábado 15 de agosto...
y no el sábado 14 de agosto como se publicó en MaTeTaM. Una disculpa por el error.
Los saluda
jmd
PD: y bueno, el resto de la información está correcta: es decir
a las 9 AM en las instalaciones de la UAMCEH-UAT (en Cd Victoria, Tamaulipas)
Segmentos iguales y colinealidad
Sea ABC un triangulo, M el punto medio de CA, P el punto donde la bisectriz desde C intersecta a AB; E y Q son los puntos donde una ceviana desde A intersecta a la bisectriz y al lado BC, respectivamnete (Q no esta en la prolongacion de BC). Demuestra que los segmentos PQ y CQ son iguales, si y solo si B, E y M son colineales.
Letracidad matemática
Introducción
Según el segundo informe PISA para los resultados de su examen del año 2000 (Literacy Skills for the World of Tomorrow - Further results from PISA 2000), la letracidad matemática se refiere a "la capacidad de identificar, comprender, e involucrarse en las matemáticas y elaborar juicios bien fundados acerca del papel que las matemáticas desempeñan para satisfacer las necesidades del individuo en su vida privada presente y futura, su vida ocupacional y social con colegas y familiares, y su vida como ciudadano constructivo, comprometido y reflexivo."
