Publicaciones Recientes
Tablero y fichas de dominó
¿Se podrá llenar de fichas de dominó el tablero de ajedrez sin cubrir dos casillas en esquinas opuestas?
Nota. Las fichas de dominó cubren exactamente dos casillas del tablero.
Hagamos un trato (Let's make a deal –The Monty Hall Paradox)
Suponga que en un show de la televisión usted está participando y el animador le da a elegir tres puertas: lo que hay detrás de la elegida es suyo. Detrás de una de ellas está un auto nuevo, detrás de las otras dos una chiva. Imagine que usted elige una de las puertas, digamos la 1, y en ese momento (antes de abrirla) el conductor, quien sabe qué hay detras de cada puerta, abre una de las dos restantes, digamos la 3, y resulta que ahí hay una chiva. A continuación te pregunta “¿deseas cambiar tu elección (abrir la puerta 2)?”
¿Te conviene cambiar?
un problema de digitos y divisibilidad
Encontrar todos los números de cuatro cifras $abcd_{10}$ divisibles entre 13 y tales que $cd =3(ac+2)$
Una sucesión no acotada
Considere la sucesión $a_0, a_1, a_2,\dots $ de enteros construida como sigue:
-
$ a_0 > 5 $ es impar,
-
$ a_{n+1} = a_n/2 $ si $ a_n $ es par,
-
y $a_{n+1} ={a_n}^2-5$ si $ a_n $ es impar.
Demostrar que la sucesión es no acotada.
USAMTS (Problema 5)
Sea c un número real. La sucesión $a_1,a_2, a_3,\dots$ está definida por $a_1=c$ y $a_n = 2a_{n-1}^2 -1$ , para todo $n \geq 2$ . Encontrar todos los valores de para los cuales $a_n <0$ para toda n.
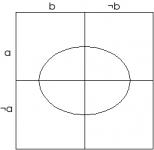
Diagrama de Lewis Carroll
Es una variante del diagrama de Venn-Euler que facilita la clasificación de un universo $S$de objetos según tres atributos $a$, $b$ y $c$. La clasificación es dicotómica: cada objeto de $S$ ya sea tiene la propiedad o atributo $a$, $b$, o $c$ o bien no la tiene (esto último se representa con ¬$a$, ¬$b$, o ¬$c$).
Triángulo Rectángulo 2
Sea ABC un triángulo rectángulo con ángulo recto en C, denotemos con R al punto donde la circunferencia inscrita es tangente al lado BC. Pruebese que $ AR \cdot RB $ es igual al área de ABC.
Retroducción en un problema de números
Al estudiante A se le da a conocer un número a y la información de que a es el producto xy de dos enteros positivos. Al estudiante B se le da a conocer un número b y la información de que es la suma x+y de los mismos números cuyo producto es el número dado a A. Además, a ambos se les hace saber que x, y son números enteros mayores que 1 y su suma es menor que 100. Después de que los estudiantes obtienen esta información (y después de haberla meditado un rato) tiene lugar el siguiente diálogo:
