Publicaciones Recientes

Sea $ABC$ un triángulo equilátero. Sean $A_1$, $B_1$ y $C_1$ puntos interiores de $ABC$ tales que $BA_1$ = $A_1C$, $CB_1$ = $B_1A$, $AC_1$ = $C_1B$ y <$BA_1C$ + <$CB_1A$ + <$AC_1B$ = 480°. 

Las rectas $BC_1$ y $CB_1$ se cortan en $A_2$, las rectas $CA_1$ y $AC_1$ se cortan en $B_2$, y las rectas $AB_1$ y $BA_1$ se cortan en $C_2$. 

Demuestra que si el triángulo $A_1B_1C_1$ es escaleno, entonces los tres circuncírculos de los triángulos $AA_1A_2$, $BB_1B_2$ y $CC_1C_2$ pasan todos por dos puntos comunes. 

NOTA: un triángulo escaleno tiene sus 3 longitudes de lados distintos.

Sean $x_1$, $x_2$, ..., $x_{2023}$ números reales positivos, todos distintos entre sí, tales que

$a_n$ = $\sqrt{(x_1 + x_2 + ... + x_n)(\frac{1}{x_1} + \frac{1}{x_2} + ... + \frac{1}{x_n})}$
 

es entero para todo $n$ = 1, 2, ..., 2023. Demuestra que $a_{2023} \geq 3034$.

Sea $ABC$ un triángulo acutángulo con $AB < AC$. Sea Ω el circuncírculo de ABC. Sea S el punto medio del arco $CB$ de Ω que contiene a A. La perpendicular por $A$ por $BC$ corta al segmento $BS$ en $D$ y a Ω de nuevo en E ≠ A. La paralela a $BC$ por $D$ corta a la recta $BE$ en $L$. Sea ω el circuncírculo del triángulo $BDL$. Las circunferencias ω y Ω se cortan de nuevo en P ≠ B. Demuestra que la recta tangente a ω en P corta a la recta BS en un punto de la bisectriz interior del ángulo <$BAC$.

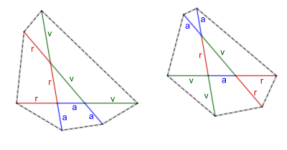
Se tienen nueve palitos de madera: tres azules de longitud $a$ cada uno, tres rojos de longitud $r$ cada uno y tres verdes de longitud $v$ cada uno, tales que es posible formar un triángulo $T$ con palitos de colores distintos.

Dana puede formar dos arreglos, comenzando con $T$ y utilizando los otros seis palitos para prolongar los lados de $T$, como se muestra en la figura. De esta manera se pueden formar dos hexágonos cuyos vértices son los extremos de dichos seis palitos. Demuestra que ambos hexágonos tienen la misma área.