Trigonometría

Se tienen nueve palitos de madera: tres azules de longitud $a$ cada uno, tres rojos de longitud $r$ cada uno y tres verdes de longitud $v$ cada uno, tales que es posible formar un triángulo $T$ con palitos de colores distintos.

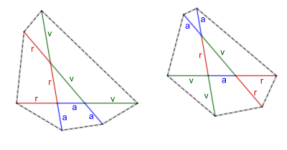
Dana puede formar dos arreglos, comenzando con $T$ y utilizando los otros seis palitos para prolongar los lados de $T$, como se muestra en la figura. De esta manera se pueden formar dos hexágonos cuyos vértices son los extremos de dichos seis palitos. Demuestra que ambos hexágonos tienen la misma área.

Sea $A_1A_2\ldots A_8$ un octágono convexo, es decir, un octágono donde todos sus ángulos internos son menores de $180^{\circ}$. Además los lados del octágono tienen la misma longitud y cada par de lados opuestos son paralelos. Para cada $i=1,\ldots,8$, definamos el punto $B_i$ como la intersección del segmento $A_iA_{i+4}$ con el segmento $A_{i-1}A_{i+1}$, donde  $A_{j+8}=A_j$ y $B_{j+8}=B_j$ para todo número entero $j$. Muestra que para algún número $i$, de entre los números $1,2,3,4$ se cumple

$$\frac{|A_iA_{i+4}|}{|B_iB_{i+4}|}\leq\frac{3}{2}$$

Sea $ABC$ un triángulo equilátero y $\Gamma$ su círculo inscrito. Si $D$ y $E$ son puntos de los lados $AB$ y $AC$, respectivamente, tales que $DE$ es tangente a $\Gamma$, demuestre que  $$\frac{AD}{DB}+\frac{AE}{EC}=1$$

Sean $x, y, z$ tres números reales tales que $0 < x < y < z < \pi/2$. Demostrar la desigualdad:
$$\pi/2 + 2\sin x\cos y + 2\sin y \cos z\gt \sin 2x + \sin 2y + \sin 2z$$

Sea $ABC$ un triángulo cuyos lados son $a, b, c$. Se divide cada lado del triángulo en "n" segmentos iguales. Sea $S$ la suma de los cuadrados de las distancias de cada vértice a cada uno de los puntos de división del lado opuesto distintos de los vértices. Demuestre que $$\frac{S}{a^2+b^2+c^2}$$ es un número racional.

 Sea $P$ un punto interior al triángulo equilátero $ABC$ tal que:
$$PA = 5, PB = 7, PC = 8$$
Encontrar la longitud del lado del triángulo ABC.