Publicaciones Recientes
Pensamiento lateral (¡¿Alguien me puede explicar eso?!)
Me he encontrado en estos días con el tema del pensamiento lateral y, sobre todo, con sus acertijos. Y creo que puede ser de alguna utilidad para los lectores de MaTeTaM una discusión sobre esos acertijos y su relación con los chistes y los problemas de matemáticas de concurso. La clave que los une es la interpretación de unos datos desde un cierto punto de vista.
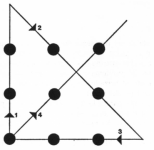
Inferencias con diofantina y clases residuales
r,r+p,r+2p primos , r=?
3.N. Encontrar todos los números primos que pueden escribirse como la diferenciade dos primos y como la suma de dos primos. (Nota: el 1 no es primo.)
Un problema guiado --de geometría
2.G. Sean ABC un triángulo isósceles con AB=AC, y P en AB y Q en AC puntostales que AP=CQ. Sea O la intersección de las mediatrices de PQ y AC.
a) Demostrar que APO y CQO son triángulos congruentes.
b) Demostrar que APOQ es un cuadrilátero cíclico.
c) Demostrar que AO es bisectriz del ángulo BAC.
(Nota: Para el inciso b puedes usar el resultado del a (sin demostración); para el cpuedes usar los resultados de a y b.)
¿Cuál fórmula? ¡Genera la lista!
1.C. ¿Cuántos números del 10 al 99 son tales que sus dígitos están en orden decreciente? Nota: 31 cumple pero no el 44 ni el 56.
XXVIII OMM Preselección Tamaulipas
Hoy viernes 30 de mayo se celebró en las instalaciones de la UAMCEH-UAT el concurso estatal OMM Tamaulipas 2014. La lista de los preseleccionados es la siguiente:
NOMBRE INSTITUCIÓN LUGAR PTS
Coeficientes y raíces en tres cuadráticas
2.6. Considere las ecuaciones cuadráticas
x2−b1x+c1=0x2−b2x+c2=0x2−b3x+c3=0
con b1.b2,b3,c1,c2,c3 números reales diferentes.
¿Es posible que los números b1,b2,b3,c1,c2,c3 sean las raíces de las ecuaciones cuadráticas en algún orden?
Configuración con acutángulo isósceles
2.5. Sea ABC un triángulo acutángulo isósceles con AC=BC. M y N son los puntos medios de AC y BC, respectivamente. La altura desde A corta a la prolongación de MN en X y la altura desde B corta a la prolongación de MN en Y. Z es la intersección de AY con BX. Además, sucede que los triángulos ABC y XYZ son semejantes. Determina la razón ACAB.
Tabla con números sin 3 o 7
2.4. Se tiene una tabla con siete columnas A,B,C,D,E,F,G y se coloca en ella los números naturales que no contienen al 3 o al 7 en su desarrollo decimal. Se empieza en la casilla C1, como se muestra. ¿En cuál columna y renglón queda el 2014?

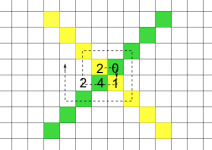
Espiral con el 2014 en cuadrícula
2.3. Sobre una cuadrícula se coloca 2014 veces el número 2014 (un dígito en cada casilla) siguiendo una espiral como se muestra en la figura. Sea M la suma de los números sobre las casillas verdes y N la suma de los números sobre las casillas amarillas. Calcula la diferencia entre M y N.