Método de áreas (2a parte)

En este post voy a discutir el método de áreas en el problem solving de matemáticas de concurso. El tema ya lo había discutido (un poco de manera reticente) en el post Método de áreas. En esta ocasión voy a profundizar un poco más en ese método, presentando y demostrando un teorema --y algunas de sus instancias de uso.

Método de áreas y razones de segmentos

Las razones de segmentos de lados de un triángulo se presentan de manera recurrente en el problem solving de geometría. Por ejemplo, en el teorema de Ceva y en el teorema de la bisectriz. Es por eso que puede resultar de alguna utilidad aprender un método más o menos general para resolver problemas de razones, atrayéndolos hacia las áreas de triángulos --en donde el problema pueda ser resuelto con menos dificultad.

En su forma elemental, el método de áreas apela a la idea de que el área de un triángulo $ABC$ es una función de la base y la altura. Si denotamos --como es usual en olimpiada de matemáticas-- el área del triángulo $ABC$ con $(ABC)$, entonces ésta está dada por la fórmula $$(ABC)=\frac{1}{2}bh$$

Y si alguna de las dos literales está fija, entonces el área del triángulo es directamente proporcional a la otra. Esta es la idea de algunas demostraciones de teoremas básicos de geometría:

Si dos triángulos tienen sus bases $BC$ y $B'C'$ sobre una recta y su tercer vértice ($A$ y $A'$) está sobre una paralela (o es común a ambos), entonces su altura es la misma y sus áreas dependen solamente de la base. De aquí que $(ABC)=BC(h/2)$ y $(A'B'C')=B'C'(h/2)$ y la razón de sus bases es igual a la razón de sus áreas.

Instancia de uso (teorema de la bisectriz)

Si la bisectriz del ángulo $A$ del triángulo $ABC$ corta al lado $BC$ en $D$, entonces se cumple
$$\frac{AB}{AC}=\frac{BD}{CD}$$

Demostración

La siguiente demostración se basa en el método de áreas y el lector queda invitado a valorar su eficacia en el problem solving degeometría.

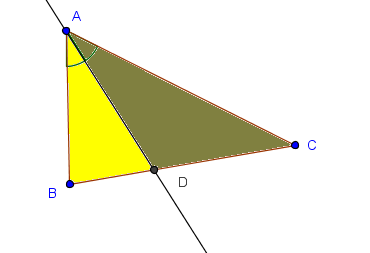
La bisectriz $AD$ divide al triángulo $ABC$ en otros dos: $ABD$ y $ACD$. Respecto a sus bases $CD$ y $BD$, los dos triángulos $ABD$ y $ACD$ tienen la misma altura. De ahí que la razón de sus áreas sea igual a la razón de sus bases: $(ABD)/(ACD)=BD/CD$.

Pero calculando su área de otra forma, y tomando en cuenta que el punto $D$ es equidistante de las bases $AB$ y $AC$, la razón de sus áreas es $AB/AC$. De ahí el resultado.

(Obviamente, más acá del método de áreas, está el hecho de que el área calculada para un triángulo debería ser la misma independientemente del procedimiento usado. Calcular de dos formas para establecer una ecuación es una estrategia de resolución de problemas que atraviesa todas las matemáticas --ver, por ejemplo, la estrategia de doble conteo en combinatoria)

Instancia de uso (bisectriz exterior)

Si la bisectriz exterior del ángulo $A$ del triángulo $ABC$ corta a la prolongación de la base $BC$ en $E$, entonces se cumple
$$\frac{AB}{AC}=\frac{BE}{CE}$$

Demostración

La bisectriz del ángulo externo en $A$ forma dos triángulos a partir del $ABC$: el triángulo $AEC$ y el triángulo $AEB$ (aunque traslapados). De nuevo, vamos a calcular la razón de sus áreas de dos formas. Viéndolos según sus bases $EC$ y $EB$, ambos tienen la misma altura pues comparten el vértice $A$. De aquí que
$$\frac{(ABE)}{(ACE)}=\frac{BE}{CE}$$

Y si los vemos según sus bases $AC$ y $AB$, ocurre lo mismo (ambos tienen la misma altura). Pues es una propiedad de la bisectriz el que sus puntos sean equidistantes de los lados. (Es una curiosidad cognitiva el hecho de que hay que tener presente esta propiedad para poder concluir alturas iguales --dado que los pies de las alturas están en la prolongación de las bases.) De aquí que
$$\frac{AB}{AC}=\frac{(ABE)}{(ACE)}$$

De ahí el resultado.

Instancia de uso (Tales)

En el triángulo $ABC$, sean $D$ y $E$ puntos en los lados $AB$ y $AC$, respectivamente. Entonces $AD/DB=AE/EC$ si y sólo si $DE//BC$.

Demostración (por áreas)

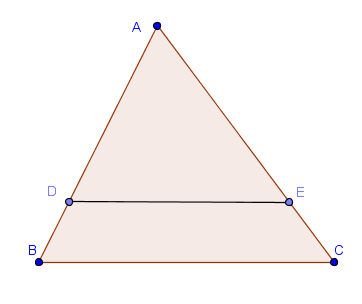
$AD/DB=AE/EC$ si y sólo si $AB/DB=AC/EC$

Pero, por el método de áreas, $AB/DB=(ABC)/(DBC)$ y $AC/EC=(ACB)/(ECB)$

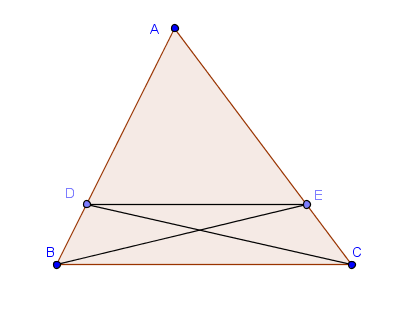
Así que $(ABC)/(DBC)=(ACB)/(ECB)$ si y sólo si (BCD)=(BCE). Y esto sucede si y sólo si los triángulos $BCD$ y $BCE$ tienen la misma altura. Es decir, si y sólo si $DE$ es paralela a $BC$.

Teorema de los segmentos cruzados

Este teorema lo vi en un documento de entrenamiento de la selección de Hong Kong (las gracias les sean dadas) y me parece que vale la pena compartirlo con los usuarios de MaTeTaM. Obviamente es de nivel avanzado, en el sentido de que no es tan intuitivo como el principio discutido arriba. Dice así:

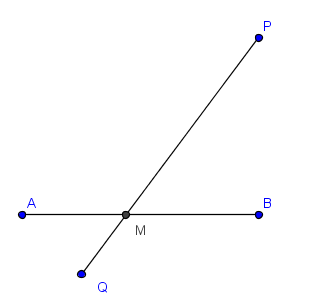
Si los segmentos $AB$ y $PQ$ (o sus prolongaciones) se cortan en $M$, entonces
$$\frac{(ABP)}{(ABQ}=\frac{PM}{QM}$$

Demostración

A manera de ilustración se presentan las figuras de los cuatro casos posibles:

1) Los dos segmentos se cortan en $M$

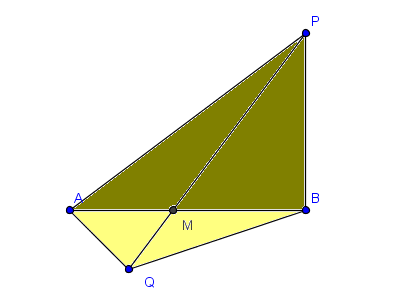
2) El segmento $AB$ corta en $M$ a la prolongación de $PQ$

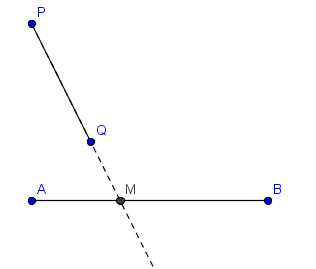
3) La prolongación de $AB$ corta en $M$ al segmento $PQ$

4) Las prolonlongaciones de ambos segmentos se cortan en $M$

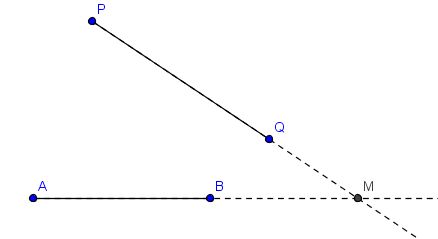
La demostración se basa en el caso recién presentado en que dos triángulos tienen un vértice común y sus bases en una misma recta. Se supondrá que ninguno de los triángulos considerados es degenerado.

Por lo demás, el lector podrá verificar fácilmente que la demostración es la misma para cada uno de los cuatro casos mencionados arriba. De esta manera, conviene tener en mente (para guiar el razonamiento) el caso prototipo en que $AB$ y $PQ$ son las diagonales del cuadrilátero $APBQ$ y $M$ su intersección.

Inicio de la prueba

$$\frac{(ABP)}{(ABQ)}=\frac{(ABP)}{(AMP)}\frac{(AMP)}{(AMQ)}\frac{(AMQ)}{(ABQ)}=\frac{AB}{AM}\frac{PM}{QM}\frac{AM}{AB}=\frac{PM}{QM}$$

Fin de la prueba

Instancia de uso: suma de razones

Sea $P$ un punto en el interior de un triángulo $ABC$, y suponga que los rayos $AP,BP,CP$ cortan a los lados $BC,CA,AB$ en los puntos $D,E,F$, respectivamente. Demostrar que
$$\frac{PD}{AD}+\frac{PE}{BE}+\frac{PF}{CF}=1$$

Demostración

La suma sugiere abordarla con áreas. Cada una de las razones de la suma es el lado derecho de la fórmula del teorema: la prolongación de $AP$ corta en $D$ al segmento $BC$, la prolongación de $BP$ corta en $E$ al segmento $CA$; la prolongación de $CP$ corta en $F$ al segmento $AB$.

De aquí que los lados izquierdos de la fórmula sean, respectivamente:
$$\frac{(BCP)}{(BCA)},\frac{(CAP)}{(CAB)},\frac{(ABP)}{(ABC)}$$
Así que, al sumar tenemos como denominador común el área de todo el triángulo y el numerador es la suma de los triángulos que los lados del $ABC$ forman con $P$. Y suman $(ABC)$. De ahí el resultado.

Instancia de uso: teorema de Ceva

Si en un triángulo $ABC$, los puntos $D,E,F$ en los lados $BC,CA,AB$, respectivamente, son tales que las cevianas $AD,BE,CF$ concurren en en el punto $P$, entonces se cumple la ecuación
$$\frac{BD}{DC}\frac{CE}{EA}\frac{AF}{FB}=1$$

Demostración

De nuevo, usando el teorema, es posible interpretar las razones de segmentos como en el problema anterior: la prolongación de $AP$ corta en $D$ al segmento $BC$, la prolongación de $BP$ corta en $E$ al segmento $CA$; la prolongación de $CP$ corta en $F$ al segmento $AB$. De aquí que las razones de segmentos se puedan sustituir por razones de áreas:
$$\frac{(APB)}{(APC)}\frac{(BPC)}{(BPA)}\frac{(CPA)}{(CPB)}$$
Y claramente, al cancelar magnitudes el resultado es la unidad.

Comentario final

Notemos, en estas instancias de uso del método de áreas, que es necesario tener una interpretación de la fórmula de reversa. Es decir, en el teorema de los segmentos cruzados se dan los dos segmentos y el punto de su intersección. Pero en problemas lo que tenemos son las razones de áreas o de segmentos y a partir de esos datos hay que reconstruir cuales segmentos se cortan en qué punto.

Por ejemplo, una razón en Ceva es $BD/DC$. Notando que el punto en común de esos segmentos es $D$, esa razón se puede poner como $BD/CD$. De aquí que sea posible interpretar que el segmento $BC$ es el $PQ$ del teorema. Es decir, $BD/CD=(APB)/(APC)$.

Este teorema es un ejemplo del hecho de que, en el problem solving, no basta con saber el teorema. Porque todavía falta interpretarlo en el contexto del problema.

Los saluda

jmd