Blogs

El problema de edades del post de las 11 preguntas de ENLACE se puede responder sin álgebra, es decir, sin manipulacones algebraicas. Este hecho me llevó a redactar el presente post, el cual puede ser de alguna utilidad para los adolescentes interesados en las matemáticas. El post presenta varios problemas razonados clásicos. Las soluciones aquí presentadas representan una curiosidad de razonamiento lógico, basado en inferencias a partir de los datos y manteniendo la simbolización a un mínimo. 

La prueba ENLACE se aplica en abril. Por esa razón MaTeTaM ha decidido dedicarle alguna atención como una forma de apoyar a los profesores y alumnos que ya iniciaron o están por iniciar su preparación para esa importante Evaluación Nacional del Logro Académico en Centros Escolares.

Si bien en la escuela mexicana no es necesaria la eficacia en el problem solving, ésta sí es relativamente importante en los exámenes estandarizados que miden actualmente el desempeño escolar de los adolescentes en matemáticas. Por ejemplo el examen ENLACE --Evaluación Nacional del Logro Académico en Centros Escolares. (ENLACE es importante pues se trata de una mirada externa al quehacer de la escuela y, con un poquito de vergüenza, es muy difícil ignorar su importancia.) 

En este post se discuten cuatro problemas de geometría analítica de ENLACE 2010 y se recomiendan algunas estrategias de resolución que han probado su eficacia en la práctica.  

ENLACE bachillerato (vive la experiencia on line)

En estos días me puse a resolver el examen en línea ENLACE Bachillerato 2010 y puedo decirles que no está de "enchílame otra". Para empezar les diré que es excesivamente largo: me tomó todo un día resolverlo (dentro de la rutina hogareña de un domingo --es decir, con salidas al centro, visitas, etc.).

Sean $l$ una recta cualquiera en el plano cartesiano y $A=(x_1,y_1)$ un punto sobre ella. Como la recta se define a través de su pendiente, se tiene que considerar el caso especial en que la pendiente no está definida por la división entre cero (caso de la recta vértical). Así pues:

Este post introduce los conceptos más básicos de la geometría analítica: distancia entre dos puntos, pendiente de una recta y coordenadas del punto medio. Supone que el lector ya conoce las reglas de representación de puntos en el plano cartesiano de coordenadas.

(Son los mejores deseos de MaTeTaM para este año y los siguientes... por lo menos 6 --para las Matemáticas en Tamaulipas.)

En este post de bienvenida al 2011, el cual es de matemáticas sólo de manera indirecta, reconozco como muy buenas las primeras jugadas del ingeniero Egidio Torre Cantú (el flamante gobernador de Tamaulipas), en particular el nombramiento de Diódoro Guerra Rodríguez como secretario de educación en Tamaulipas. 

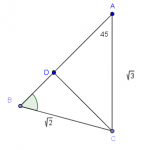
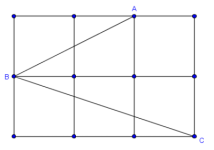
 Hablando en general, la solución de un problema de geometría exige cierta creatividad. Ésta, con frecuencia, consiste en ver el problema de otra forma. Por ejemplo, ampliando el contexto mediante un trazo auxiliar.

Se trata del fenómeno del framing  el cual he abordado en otros posts en MaTeTaM. Framing se traduce como encuadre o enmarcamiento, como cuando se le pone el marco a una fotografía o pintura. Así pues, la creatividad, con frecuencia, consiste en poner al problema en un marco adecuado.

En este post sugiero la razón  por la que una de las recomendaciones de la OCDE para evitar el triste futuro (y presente) educativo de México es imposible de realizar, e incluyo uno de los problemas de matemáticas de PISA 2009, la evaluación internacional de la OCDE que mide el estado de la educación de los países miembros.

 El problema 1 de la 24 OMM resultó ser un hueso duro de roer --para los concursantes que no conocían algunos trucos de acotación. Su enunciado parece tan inocente... "Encuentra todas las ternas de números naturales $(a,b,c)$ que cumplan la ecuación $abc=a+b+c+1$." Pero su inocencia aparente es una inocencia envenenada.