Básico
Factorizar y resolver
Encontrar todas las soluciones $(x,y)$ en enteros positivos de la ecuación diofantina $x^3=19+y^3$
Pudorosa (segunda parte)
Decidir --con prueba-- si la ecuación diofantina $123x+426y=8$ tiene solución.
Una pudorosa propiedad del máximo común divisor
Si $a, b$ son enteros y cumplen $7a-38b=-2$ ¿qué se puede concluir sobre el máximo común divisor de a y b?
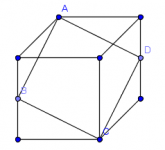
Cuadrilátero en un cubo
En un cubo de arista 6 los puntos medios B,D de dos aristas opuestas, y dos vértices opuestos A,C pero no en las aristas de los puntos medios B,D, forman un cuadrilátero ABCD. Encontrar el área de ese cuadrilátero.
¿Es múltiplo de 11? (Que lo diga Fermat.)
Decidir --con prueba-- si $61^{61}+71^{71}$ es divisible entre 11.
ExSel2_Pr1: Inclusión y exclusión... pero basta con razonarlo
¿Cuántos números enteros positivos no mayores que 1000 no son ni cuadrados ni cubos?
Progresión aritmética con un cuadrado
Demostrar que si una progresión aritmética de enteros positivos contiene un cuadrado perfecto entonces contiene infinitamente muchos cuadrados perfectos.
Los primos no se factorizan... excepto en la forma 1( p )
Encontrar todos los enteros positivos n tales que $n^{20}+n^{10}+1$ es un primo.
Semicírculo y la descomposición en dos sumandos de un segmento.
Sea $$BC$ el diametro de una semicirculo y sea $A$ el punto medio del semicirculo. Sea M un punto sobre el arco $AC$. Seam $P$ y $Q$ los pies de las perpendiculares desde $A$ y C a la linea $BM$, respectivamente.
Demustra que $BP=PQ+QC$
Áreas enteras de triángulos
El área del triángulo $ ABC $ es un entero. Sobre los lados $ BC$ y $AC$ se eligen los puintos $X$ y $Y$, respectivamente. Los segmentos $AX$ y $ BY$ se cortan en un punto $P$ dentro del triángulo $ ABC $. El área de $BPX$ es 1, la de $APY$ es 2, y la de $APB$ es un entero. Encontrar el área del triángulo $ABC.$
